Linear Algebra for Machine Learning and Data Science

This series of blog posts aims to introduce and explain the most important mathematical concepts from linear algebra for machine learning. If you understand the contents of this series, you have all the linear algebra you’ll need to understand deep neural networks and statistical machine learning algorithms on a technical level. Most of my examples reference machine learning to give you an understanding of how mathematical concepts relate to practical applications. However, the concepts are domain-agnostic. So, if you come from a different domain, the explanations are hopefully still useful for you.

Here’s an overview in chronological order.

• Basic Vector Operations
• Unit Vector
• Dot Product and Orthogonal Vectors
• Linear Independence
• Vector Projections
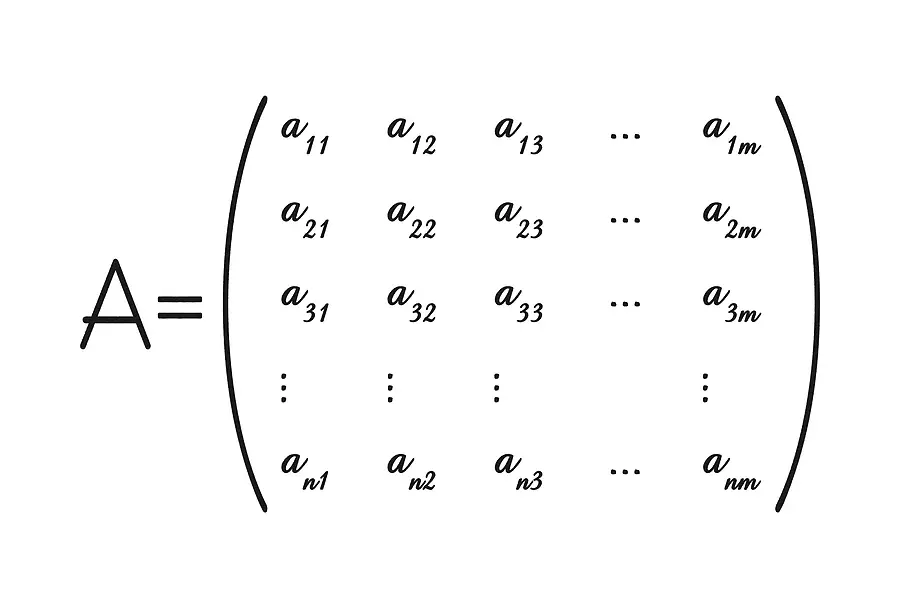
• Basic Matrix Operations
• Matrix Multiplication
• Transformation Matrix
• Determinant of a Matrix
• Gauss Jordan Elimination
• Diagonal Matrix
• Identity Matrix and Inverse Matrix
• Transpose Matrix
• Orthogonal Matrix
• Change of Basis Matrix
• Gram Schmidt Process
• Eigenvectors
• Eigenvalue Decomposition
• Singular Value Decomposition

For writing these posts I’ve relied on the following books:

Further Resources

For writing these posts I’ve relied on several textbooks, online courses, and blogs.

Here you find a comprehensive list of resources that I’ve used to write these posts and that I recommend for further study.

I regularly write on machine learning, data science, math, and statistics. So stay tuned and sign up to my email list for updates!