Singular Value Decomposition Explained

In this post, we build an understanding of the singular value decomposition (SVD) to decompose a matrix into constituent parts.

What is the Singular Value Decomposition?

The singular value decomposition (SVD) is a way to decompose a matrix into constituent parts. It is a more general form of the eigendecomposition. While the eigendecomposition is limited to square matrices, the singular value decomposition can be applied to non-square matrices.

How to perform a Singular Value Decomposition?

Specifically, the SVD decomposes any matrix A into an orthogonal matrix U, a diagonal matrix Σ, and another orthogonal matrix V^T.

A = UΣV^T

U consists of the eigenvectors of AA^T, while V is a matrix of eigenvectors of A^TA. The singular values in Σ are the square root of the eigenvalues of AA^T.

Remember that the eigendecomposition can only be performed on square matrices. By multiplying A by its transpose, you get a matrix that has the same number of rows as columns, and you can perform the eigendecomposition. U is also known as a matrix of left-singular vectors, Σ as the singular values, and V^T as the right singular vectors. Phew….that’s a lot to digest.

Luckily, you’ll probably never have to calculate this by hand since computers will do it for you. Therefore, I’m not going to through a manual example. Instead, I’ll focus on a more conceptual understanding of the SVD. If you are interested in how we get from AA^T to the SVD, I highly recommend checking out the following by Gilbert Strang.

As we’ve discussed in the chapter on the eigendecomposition, applying repeated operations to a diagonal matrix is much easier and computationally less expensive than applying it to non-diagonal ones.

The matrices U and V are column-orthogonal, which means all matrices U, Σ, and V^T are linearly independent. This is extremely important in data science and machine learning because it allows you to conceptually separate information into distinct and independent concepts.

Singular Value Decomposition Example

Imagine you had a grocery store selling different products, and you captured all your products as columns in a matrix and all customers as rows. Every row indicates how many items of a certain product a consumer has bought. We assume that buying larger amounts of a certain product indicates a greater preference.

I’ve calculated this using a software package in Python. Usually, such decompositions are done by a computer, so it is much more important to have a conceptual understanding of what the SVD does rather than being able to calculate it by hand.

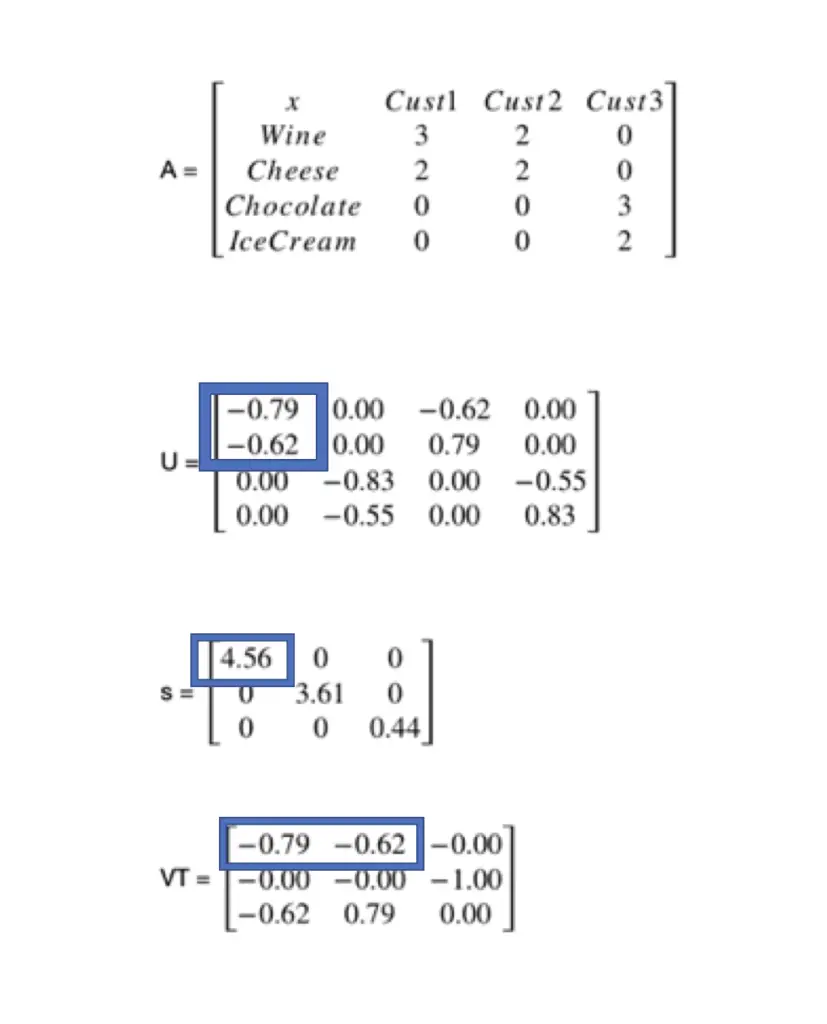
You can think of U as representing the similarity of various products to certain concepts.

V^T encapsulates a concept such as a “wine lover” or a cheese lover, while Sigma (s) represents the strength of that concept.

In this case, it seems to me that there must be something like a “french gourmand” who likes wine and cheese but who doesn’t like sweets and a sweet lover who doesn’t like wine and cheese. The first two column entries in U indicate that wine has a high similarity to the concept of a French gourmand. Sigma shows us that this seems to be a strong concept, and V^T indicates that Customers 1 and 2 strongly associate with this concept.

Summary

While it is rarely necessary to calculate the SVD by hand, a conceptual understanding is useful for many applications such as machine learning.

This post is part of a series on linear algebra for machine learning. To read other posts in this series, go to the index.