Unit Vector: Background and Definition

In this short post, we will learn how to calculate the magnitude of a vector and how to obtain the unit vector.

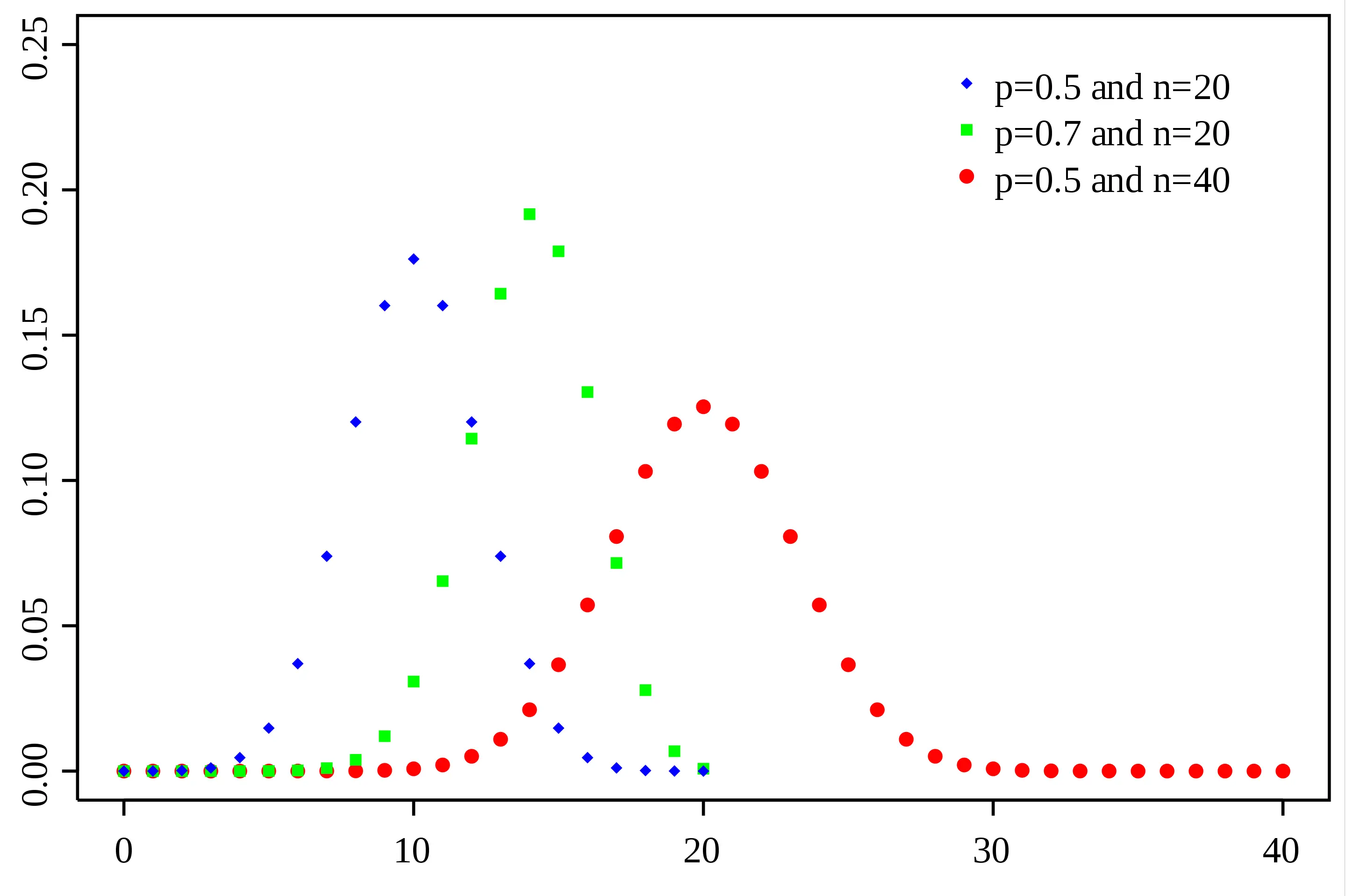
The magnitude of a Vector

A vector has a direction and a magnitude (or length). The following vector has a direction of 1 on the x-axis and 3 on the y-axis. 

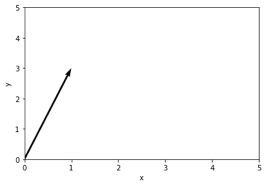
But what about the magnitude? Maybe you remember the Pythagorean theorem from school, which enables you to calculate the length of the longest side (hypotenuse) of a right-angled triangle z from the two shorter sides x and y.

x^2 + y^2 = z^2 

Our vectors

red \begin{bmatrix}1\\3\end{bmatrix}, green \begin{bmatrix}1\\0\end{bmatrix}, blue \begin{bmatrix}0\\3\end{bmatrix}

can be thought of as a right-angled triangle with vector red forming the hypotenuse and green, blue the adjacent sides.

According to Pythagoras, we arrive at the following formula for calculating the magnitude of red:

\sqrt(green_x^2 + blue_y^2) = |red| 

\sqrt{1^2 + 3^2)}= \sqrt{10}

Note on notation: a variable v denotes a vector, whereas |v| denotes the length of a vector.

What is a Unit Vector

The unit vector of a vector b is defined as a vector going in the same direction as b of length 1.

To get to a length of one for b, we only have to divide b by its length |b|. 

Unit vector formula:  

\frac{b}{|b|}

Example:

b =\begin{bmatrix}x\\y\end{bmatrix} \, \, then \, \frac{b}{|b|}
=
\frac{(x, y)}{\sqrt(x^2 + y^2)}

Plugging the numbers 3 and 4 into x and y gives us the following unit vector

b = \begin{bmatrix}3\\4\end{bmatrix}

|b| = \sqrt{3^2 + 4^2} = 5

\frac{b}{|b|} =
\begin{bmatrix}\frac{3}{5}\\\frac{4}{5}\end{bmatrix}

This post is part of a series on linear algebra for machine learning. To read other posts in this series, go to the index.