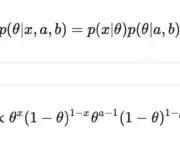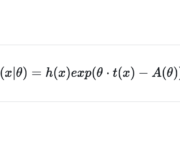Latest Posts
See what's new
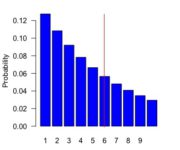
Geometric Distribution and Geometric Random Variables
On March 18, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we introduce the geometric distribution with an example and discuss how to calculate the probability of geometric random variables. The geometric distribution describes the probability of the number of failures before a successful outcome in a Bernoulli trial. Suppose you are a recruiter and you need to find a suitable candidate
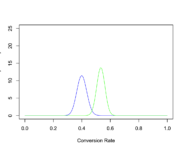
Conjugate Priors
On March 14, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we introduce the concept of conjugate priors and how they enable us to infer posterior parameters from prior distributions. The real world is messy and the probability of events is usually influenced by environmental factors. In statistics, we have methodologies for dealing with uncertainty and environmental influences such as the concept
The Beta Distribution
On March 8, 2021 In Mathematics for Machine Learning, Probability and Statistics
We build an intuitive understanding of the Beta distribution and its utility as a prior distribution for many other probability distributions. The beta distribution models a distribution of probabilities. If we don’t know the probability of the outcome of an event, we can use the beta distribution to model the distribution of probabilities given
Gamma Distribution
On March 3, 2021 In Mathematics for Machine Learning, None, Probability and Statistics
In this post we build an intuitive understanding of the Gamma distribution by going through some practical examples. Then we dive into the mathematical background and introduce the formulas. The gamma distribution models the wait time until a certain number of continuously occurring, independent events have happened. If you are familiar with the Poisson
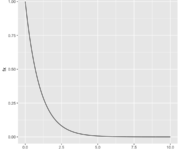
Exponential Distribution and Exponential Random Variables
On February 27, 2021 In Mathematics for Machine Learning, Probability and Statistics
We introduced the exponential distribution with a formal definition and some examples. We also learn how the exponential distribution relates to a Poisson process. The exponential distribution models the time interval between continuously occurring, independent events. In case you are familiar with the Poisson distribution, the exponential distribution models the wait time between events
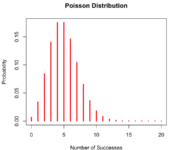
The Poisson Distribution
On February 22, 2021 In Mathematics for Machine Learning, Probability and Statistics
We introduce the Poisson distribution and develop an intuitive understanding of its uses by discussing examples and comparing the Poisson distribution to the binomial distribution. With the Poisson distribution, we can express the probability that a certain number of events happen in a fixed interval. Poisson Distribution Examples The Poisson distribution is useful in
Central Limit Theorem
On February 15, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we build an intuitive understanding of the central limit theorem by looking at some examples. Then, we introducing the formal definition of the CLT. What is the Central Limit Theorem The central limit theorem states that under most conditions, the sum of large numbers of random variables is normally distributed. This
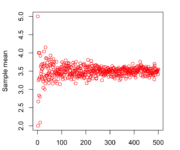
What is the Law of Large Numbers
On February 13, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we introduce the law of large numbers and its implications for the expected value and the variance. The law of large numbers states that the larger your sample size the closer your observed sample mean is to the actual population mean. Intuitively this makes sense. Suppose, you wanted to estimate the
Probability and Statistics for Machine Learning and Data Science
On February 6, 2021 In Mathematics for Machine Learning, None, Probability and Statistics
This series of blog posts introduces probability and mathematical statistics. While I wrote these posts with a focus on machine learning and data science applications, they are kept sufficiently general for other readers. Some familiarity with vectors and matrices, as well as differential and integral calculus, is necessary to fully understand all concepts. If
Factorization Theorem and the Exponential Family
On February 6, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we introduce Fisher’s factorization theorem and the concept of sufficient statistics. We learn how to use these concepts to construct a general expression for various common distributions known as the exponential family. In applied statistics and machine learning we rarely have the fortune of dealing with a known distribution with known