Exponential Distribution and Exponential Random Variables

We introduced the exponential distribution with a formal definition and some examples. We also learn how the exponential distribution relates to a Poisson process.

The exponential distribution models the time interval between continuously occurring, independent events. In case you are familiar with the Poisson distribution, the exponential distribution models the wait time between events in a Poisson process.

Exponential Distribution Formula

The same rate parameter lambda defines the exponential function as the Poisson distribution. The probability density function of the exponential distribution is given by

   f(x) = \left\{
     \begin{array}{lr} 

\sigma(z) <0.5 &\quad if \; z < 0 \\
\sigma(z) >0.5 &\quad if \; z >0 \\

     \end{array}
   \right.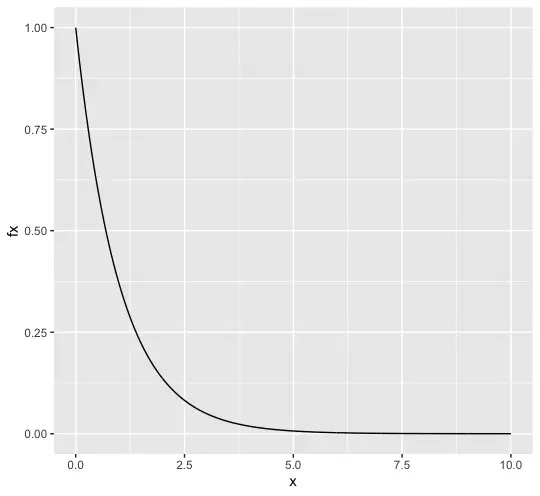

Let’s assume that this function models the wait time for a bus arriving once per hour at a bus stop. If we wanted to calculate the probability that the bus arrives two hours or later, we could plug the following values into the function.

1 \times e^{-1 \times 2} = 0.135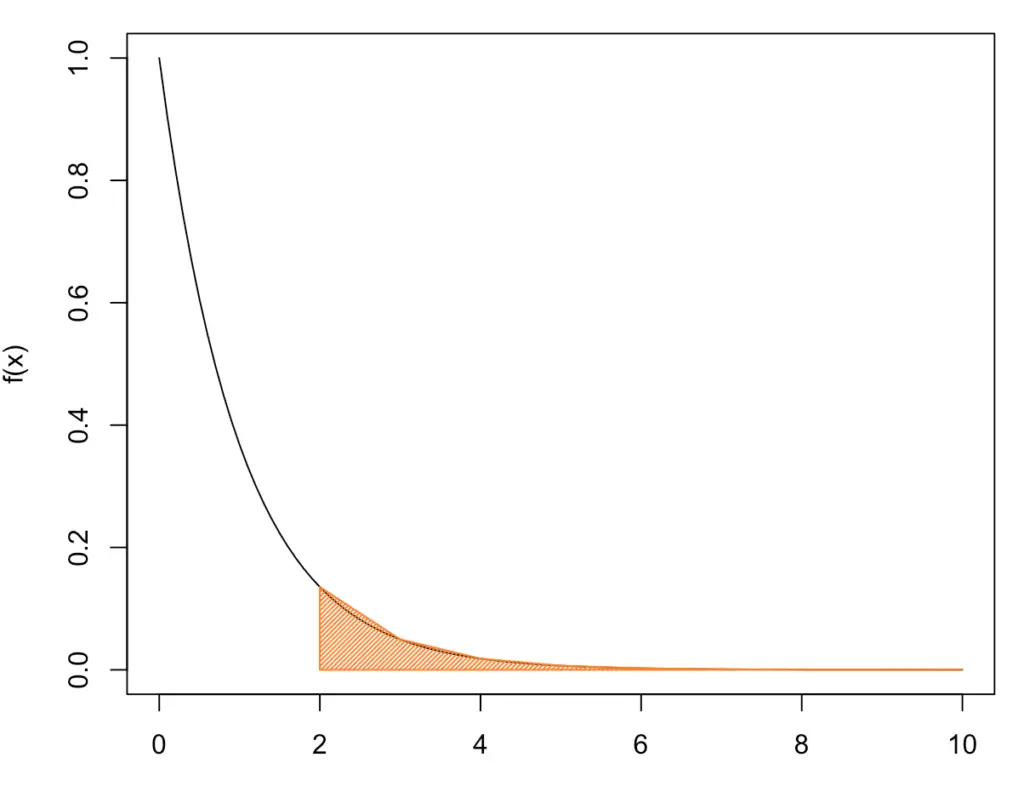

So our chance of waiting for at least two hours is roughly 13.5%.

Since this is a probability density function, we are not dealing with discrete events but with intervals. Accordingly, it doesn’t make sense to calculate the probability that the bus will arrive after exactly 2 hours.

The expected value and the variance of the exponential distribution are:

EX = \frac{1}{\lambda} \;\;\;\; Var(X) = \frac{1}{\lambda^2}

Relationship between Poisson and Exponential Distribution

In a Poisson process, that is a process where independent events occur continuously at a certain rate, the time between events follows an exponential distribution.

For example, the arrival of busses at a bus stop is a Poisson process. Busses arrive continuously, and if one of them is late, it is usually unrelated to the others. In Germany, most busses will arrive roughly on time. Some may run a few minutes late. But only very few busses will run one or two hours late.
So the time that passes between the arrival of two busses is exponentially distributed.

When examining the time between two events, we are looking at a Poisson interval in which no event has happened. This means the parameter for the Poisson event x is zero.

P(X=x) = \frac{\lambda^0 e^{-\lambda}}{0 !} 

Note: whether events have already happened before is irrelevant because Poisson events are independent. We say a Poisson process is memoryless.

Assuming that the time period in which the events occur is equal to one unit of time, we arrive directly at the exponential distribution.

P(X=x) = \frac{\lambda^0 e^{-\lambda}}{0 !} = e^{-\lambda} = 1 e^{-1\lambda} 

Exponential Distribution Examples

A common application of the exponential distribution is survival time analysis in a broader sense.

For example, the survival time of a 90-year-old follows an exponential distribution. The probability of reaching his 91st birthday is exponentially higher than the probability of reaching his 100th birthday.

Similarly, the time until a machine such as your car breaks down follows an exponential distribution.

This post is part of a series on statistics for machine learning and data science. To read other posts in this series, go to the index.