Mathematics for Machine Learning Archive
Power Series: Understand the Taylor and MacLaurin Series
On December 21, 2020 In Calculus, Mathematics for Machine Learning
In this post, we introduce power series as a method to approximate unknown functions. We derive the Maclaurin series and the Taylor series in simple and intuitive terms. Differential calculus is an amazing tool to describe changes in complex systems with multiple inputs. But to unleash the power of Calculus, we need to describe
The Multivariable Chain Rule
On December 17, 2020 In Calculus, Mathematics for Machine Learning
In this post we learn how to apply the chain rule to vector-valued functions with multiple variables. We’ve seen how to apply the chain rule to real number functions. Now we can extend this concept into higher dimensions. How does the Multivariable Chain Rule Work? Remember that the chain rule helps us differentiate nested
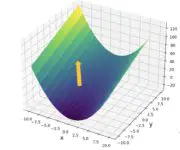
The Hessian Matrix: Finding Minima and Maxima
On December 17, 2020 In Calculus, Mathematics for Machine Learning
In this post, we learn how to construct the Hessian matrix of a function and find out how the Hessian helps us determine minima and maxima. What is a Hessian Matrix? The Jacobian matrix helps us find the local gradient of a non-linear function. In many applications, we are interested in optimizing a function.
The Jacobian Matrix: Introducing Vector Calculus
On December 16, 2020 In Calculus, Mathematics for Machine Learning
We learn how to construct and apply a matrix of partial derivatives known as the Jacobian matrix. In the process, we also introduce vector calculus. The Jacobian matrix is a matrix containing the first-order partial derivatives of a function. It gives us the slope of the function along multiple dimensions. Previously, we’ve discussed how
How to Take Partial Derivatives
On December 15, 2020 In Calculus, Mathematics for Machine Learning
We learn how to take partial derivatives and develop an intuitive understanding of them by calculating the change in volume of a cylinder. Lastly, we explore total derivatives. Up until now, we’ve always differentiated functions with respect to one variable. Many real-life problems in areas such as physics, mechanical engineering, data science, etc., can
Products, Quotients, and Chains: Simple Rules for Calculus
On December 10, 2020 In Calculus, Mathematics for Machine Learning
In this post, we are going to explain the product rule, the chain rule, and the quotient rule for calculating derivatives. We derive each rule and demonstrate it with an example. The product rule allows us to differentiate a function that includes the multiplication of two or more variables. The quotient rule enables us
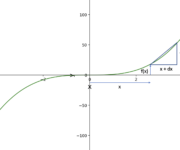
Differential Calculus: How to Find the Derivative of a Function
On December 8, 2020 In Calculus, Mathematics for Machine Learning
In this post, we learn how to find the derivative of a function from first principles and how to apply the power rule, the sum rule, and the difference rule. We previously established that the definition of a derivative equals the following expression. Note that f'(x) is a more compact form to denote the
Rise Over Run: Understand the Definition of a Derivative
On December 7, 2020 In Calculus, Mathematics for Machine Learning
We introduce the basics of calculus by understanding the concept of rise over run, followed by a more formal definition of derivatives. At the heart of calculus are functions that describe changes in variables. In complex systems, we usually deal with many changing variables that depend on each other. The concept of rise over
Singular Value Decomposition Explained
On December 4, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post, we build an understanding of the singular value decomposition (SVD) to decompose a matrix into constituent parts. What is the Singular Value Decomposition? The singular value decomposition (SVD) is a way to decompose a matrix into constituent parts. It is a more general form of the eigendecomposition. While the eigendecomposition is
Linear Algebra for Machine Learning and Data Science
On December 2, 2020 In Linear Algebra, Mathematics for Machine Learning
This series of blog posts aims to introduce and explain the most important mathematical concepts from linear algebra for machine learning. If you understand the contents of this series, you have all the linear algebra you’ll need to understand deep neural networks and statistical machine learning algorithms on a technical level. Most of my