Differential Calculus: How to Find the Derivative of a Function

In this post, we learn how to find the derivative of a function from first principles and how to apply the power rule, the sum rule, and the difference rule.

We previously established that the definition of a derivative equals the following expression.

f'(x) = \lim_{dx\to0}\frac{f(x + dx) - f(x)}{dx}

Note that f'(x) is a more compact form to denote the derivative of f(x), also known as the Lagrange notation. How can we use this to get the derivative of a function? Let’s use

5x +2

and plug it into our formal definition.

f'(x) = \lim_{dx\to0}\frac{5(x + dx) + 2 - (5x + 2)}{dx}

If we multiply this out, most terms cancel each other out. We arrive at the following expression:

f'(x)  = \lim_{dx\to0}\frac{5dx}{dx}

Now we can divide by dx, and we are left with

f'(x)   = 5

which is the derivative of 5x + 2.

Why does this work?

5x + 2 is just a linear function.

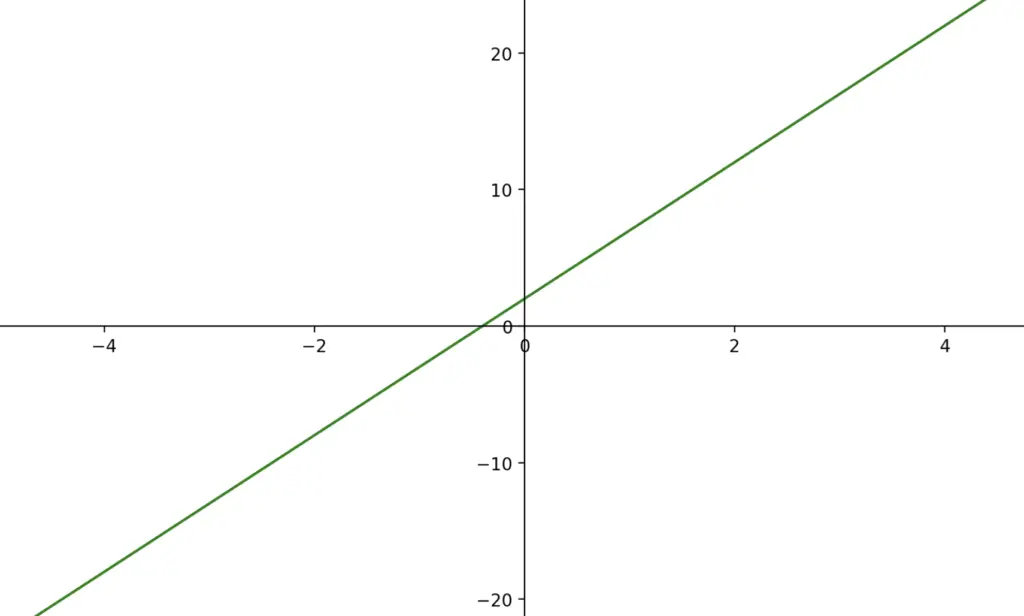
Therefore, the slope must be constant, and the derivative is nothing but the slope of the function. We don’t need a nonlinear variable like x to express the slope. The constant 2 is irrelevant for determining the slope. Accordingly, x and 2 disappear.

From this, we can deduce the more general rules

For a constant a

f'(x) = 0

For a linear function expressed by the variable x

f'(x) = 1

For a term ax

f'(x) = a

But what about Higher-Order Functions?

The Power Rule

Let’s take the function

f(x) = 5x^2 + 2

Now we obtain the derivative as follows.

f'(x) = \lim_{dx\to0}\frac{5(x + dx)^2 + 2 - (5x^2 + 2)}{dx}

f'(x) = \lim_{dx\to0}\frac{5x^2 + 2xdx + dx^2 + 2 - 5x^2 - 2}{dx} 

f'(x) = 10x + 5dx

Remember that because a higher-order function is constantly changing its slope, we need to approximate the slope at a certain point by taking the slope of an infinitely small triangle. So dx is so small that it becomes irrelevant, and we can forget about it.

f'(x) = 10x 

We can generalize this in the following rule known as the power rule:

if\\f(x) = x^a \\ then \\f'(x) = ax^{a-1}

Sum Rule and Difference Rule

Besides the Power rule, there are several more rules that can be derived from the formal definition of a derivative. I won’t derive all of them by example, but you should have seen enough by now to do this yourself. In this post, I’ll still show you the sum rule and the difference rule.

The sum rule says that differentiating a function with multiple terms is equivalent to differentiating the terms individually and then adding them up.

f + g = f' + g'

For example

f(x) = x^2 + x^3 \\
f'(x) = \frac{d}{dx} x^2 + \frac{d}{dx} x^3 \\

\frac{d}{dx} x^2 = 2x \;\:and \;\:
\frac{d}{dx} x^3 = 3x^2

Accordingly:

f'(x) = 2x + 3x^2

The same principle applies to subtracting one term from another.

f - g = f' - g'

This is known as the difference rule. Demonstrated in action, it would look like this.

f(x) = x^2 - x^3 \\
f'(x) = 2x - 3x^2

This post is part of a series on Calculus for Machine Learning. To read the other posts, go to the index.