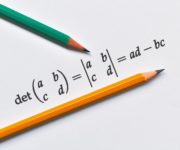Mathematics for Machine Learning Archive
Eigenvalue Decomposition Explained
On December 2, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post, we learn how to decompose a matrix into its eigenvalues and eigenvectors. We also discuss the uses of the Eigendecomposition. The eigenvalue decomposition or eigendecomposition is the process of decomposing a matrix into its eigenvectors and eigenvalues. We can also transform a matrix into an Eigenbasis (the basis matrix where every
Understanding Eigenvectors in 10 Minutes
On December 1, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post, we explain the concept of eigenvectors and eigenvalues by going through an example. What are Eigenvectors and Eigenvalues An eigenvector of a matrix A is a vector v that may change its length but not its direction when a matrix transformation is applied. In other words, applying a matrix transformation to
Gram Schmidt Process: A Brief Explanation
On November 30, 2020 In Linear Algebra, Mathematics for Machine Learning
The Gram Schmidt process is used to transform a set of linearly independent vectors into a set of orthonormal vectors forming an orthonormal basis. It allows us to check whether vectors in a set are linearly independent. In this post, we understand how the Gram Schmidt process works and learn how to use it
Understanding the Change of Basis Matrix
On November 27, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post, we learn how to construct a transformation matrix and apply it to transform vectors into another vector space. This process is also referred to as performing a change of basis. As discussed in the previous article on vector projections, a vector can be represented on a different basis than the basic
Orthogonal Matrix: Definition and Example
On November 26, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post, we introduce orthonormal bases, orthogonal matrices and discuss their properties. An orthogonal matrix is a square matrix whose rows and columns are vectors that are orthogonal to each other and of unit length. We can also say that they form an orthonormal basis. Orthonormal Basis A set of vectors V =
What is a Transpose Matrix
On November 26, 2020 In Linear Algebra, Mathematics for Machine Learning
In this short post, we learn how to obtain the transpose of a matrix and how to perform operations with a matrix transpose. The transpose of a matrix is a matrix that is obtained by flipping the original matrix over its diagonal. In other words, the rows of a matrix become the columns of
Identity Matrix and Inverse Matrix
On November 25, 2020 In Linear Algebra, Mathematics for Machine Learning
We introduce the inverse matrix and the identity matrix. In addition, we learn how to solve systems of linear equations using the inverse matrix. The identity matrix is a matrix in which the diagonal entries are 1, and all other entries are zero. It is a more restrictive form of the diagonal matrix. It
Understanding the Determinant of a Matrix
On November 24, 2020 In Mathematics for Machine Learning, None
We introduce the matrix determinant and its uses. Furthermore, we learn how the determinant provides us with a shortcut to finding the inverse matrix. What is the matrix determinant? The determinant is a scalar value that can be obtained from a square matrix and which can be used to find the inverse of a
How to Perform Matrix Multiplication
On November 23, 2020 In Linear Algebra, Mathematics for Machine Learning
In this post we learn how to perform matrix multiplication and why we need to be mindful of matrix dimensions. Furthermore, we look at the properties of matrix multiplication. Matrix multiplication is an operation that consists of the element-wise multiplication of all entries in a row of the first matrix with all entries in
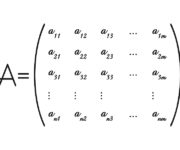
How to Perform Basic Matrix Operations
On November 22, 2020 In Mathematics for Machine Learning
We introduce and define matrices. Furthermore, we learn how to perform matrix addition and matrix subtraction. A matrix is simply a 2-dimensional vector. While vectors only have one dimension m, matrices have 2 dimensions m and n We say A is an matrix. As you can see, we usually denote matrices with capital letters.