How to Take Partial Derivatives
We learn how to take partial derivatives and develop an intuitive understanding of them by calculating the change in volume of a cylinder. Lastly, we explore total derivatives.
Up until now, we’ve always differentiated functions with respect to one variable. Many real-life problems in areas such as physics, mechanical engineering, data science, etc., can be described as functions of more than one independent variable.
A partial derivative tells us how the change in one particular variable affects the result of the function in a function with multiple variables. For example, the amount of water that flows through a pipe in a timeframe depends on the water pressure and pipe volume. Using partial derivatives, you can determine how the change in just the volume or just the pressure changes the amount of water.
How can you know how the change in one particular variable affects the system described by your function? Let’s go through an example to understand the concept:
The volume of a cylinder can be described as a function of its height h and its radius r.
V = \pi r^2 h
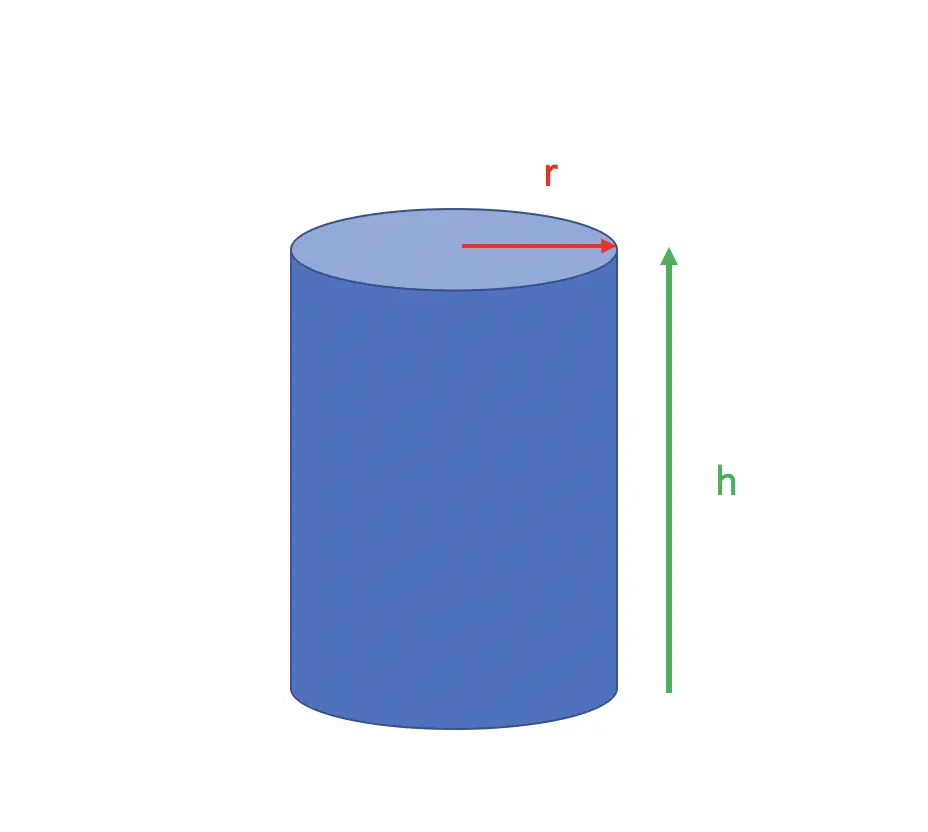
Suppose you need to describe how the volume changes in response to varying just the height while keeping the radius constant. To achieve this, you would differentiate the function describing the volume just with respect to h, treating everything else, including r, as a constant. This gives you the following expression.
V' = \pi r^2
But wait, isn’t this the formula for the area of a circle? Indeed, it is. That makes perfect sense. If you increase h by an infinitesimally small amount, it is like stacking a circle on top of the cylinder.
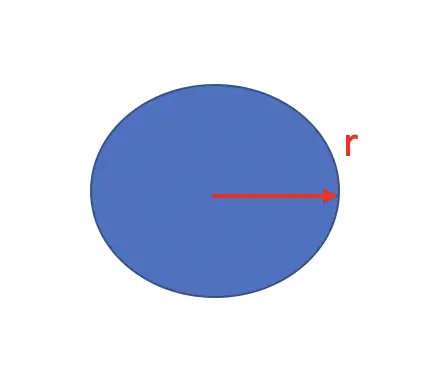
The area of the circle is equivalent to the partial derivative of V with respect to h. Formally we would say.
\frac{\partial V}{\partial h} = \pi r^2Note that \partial is the partial derivative symbol. You use it instead of d when you are differentiating a multivariate function with respect to one variable.
If we wanted to find out how V changes if we only increased or decreased r, we would take the partial derivative of V with respect to r.
V = \pi r^2 h
\frac{\partial V}{\partial r} = 2\pi rhTotal Derivative
Differentiating with respect to one variable and keeping all others constant helps manipulate complex systems in theory. But in many cases, several variables will vary simultaneously. How do we differentiate with respect to more than one variable?
You just have to differentiate the function with respect to each variable individually and then add up the resulting terms. The result is known as the total differential. For a simple function
y = u \times v
the total differential resolves to the following expression.
dy = \frac{\partial y}{\partial u} du + \frac{\partial y}{\partial v}dvIn the case of our cylinder, this means we differentiate with respect to r and h simultaneously.
\frac{\partial V}{\partial h} = \pi r^2 \\\frac{\partial V}{\partial r} = 2\pi rhdV = \pi r^2 dh + 2\pi rh dr
But how do we get rid of the dh and the dr expressions? And why do we need them in the first place?
In our little example, where we just give h and r arbitrary values, we can forget about dh and dr.
But in real applications, h and r may themselves be functions of some other variables. To arrive at the true total derivative of V, we would have to dig deeper and see how h and r change in response to some other variable. Let’s assume that h and r increase over time, so they are both dependent on time t.
r = 3t\\ h = t^2
To find out the true dV with respect to time, we would treat t as a nested variable. In the case of nested variables, we can apply the chain rule.
dV = \frac{\partial V}{\partial h} \frac{d h}{d t} + \frac{\partial V}{\partial r} \frac{d r}{d t}dV = \pi r^2 (2t) + 2\pi rh (3)
This post is part of a series on Calculus for Machine Learning. To read the other posts, go to the index.