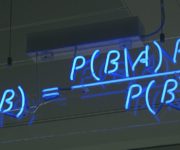Mathematics for Machine Learning Archive
Introducing Variance and the Expected Value
On January 13, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we are going to look at how to calculate expected values and variances for both discrete and continuous random variables. We will introduce the theory and illustrate every concept with an example. Expected Value of a Discrete Random Variable The expected value of a random variable X is usually its mean.
The Law of Total Probability and Bayesian Inference
On January 9, 2021 In Mathematics for Machine Learning, Probability and Statistics
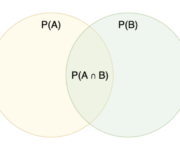
In this post we introduce the law of total probability and learn how to use Bayes’ rule to incorporate prior probabilities into our calculation for the probability of an event. Events don’t happen in a vacuum. They are related to and dependent on circumstances in their environment. Bayes rule allows us to relate the
Conditional Probability and the Independent Variable
On January 8, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we learn how to calculate conditional probabilities for both discrete and continuous random variables. Furthermore, we discuss independent events. Conditional Probability is the probability that one event occurs given that another event has occurred. Closely related to conditional probability is the notion of independence. Events are independent if the probability of
Probability Mass Function and Probability Density Function
On January 6, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we learn how to use the probability mass function to model discrete random variables and the probability density function to model continuous random variables. Probability Mass Function: Example of a Discrete Random Variable A probability mass function (PMF) is a function that models the potential outcomes of a discrete random variable.
What is a Random Variable in Statistics: An Introduction to Probability
On January 4, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we look at the basic rules of probability and the notation used to describe probabilities and probability functions. We also introduce random variables. Probability is the branch of mathematics that deals with quantifying uncertainty. To model a real-world process that does not have a deterministic outcome, we can construct a probability
Calculus For Machine Learning and Data Science
On December 31, 2020 In Calculus, Mathematics for Machine Learning
This series of blog posts introduces multivariate calculus for machine learning. While the first few posts should be accessible to anyone with a high-school math background, the articles covering vector calculus require a basic understanding of linear algebra. If you need a refresher, I’d suggest you first check out my series on linear algebra.
The Fundamental Theorem of Calculus and Integration
On December 31, 2020 In Calculus, Mathematics for Machine Learning
In this post, we introduce and develop an intuitive understanding of integral calculus. We learn how the fundamental theorem of calculus relates integral calculus to differential calculus. Integration is the reverse operation of differentiation. Together they form a powerful toolset to describe non-linear functions. While differentiation enables us to describe the gradient or rate
Lagrange Multipliers: An Introduction to Constrained Optimization
On December 28, 2020 In Calculus, Mathematics for Machine Learning
In this post we explain constrained optimization using LaGrange multipliers and illustrate it with a simple example. Lagrange multipliers enable us to maximize or minimize a multivariable function given equality constraints. This is useful if we want to find the maximum along a line described by another function. The Lagrange Multiplier Method Let’s say
Understanding The Gradient Descent Algorithm
On December 24, 2020 In Calculus, Mathematics for Machine Learning
In this post, we introduce the intuition as well as the math behind gradient descent, one of the foundational algorithms in modern artificial intelligence. Motivation for Gradient Descent In many engineering applications, you want to find the optimum of a complex system. For example, in a production system, you want to find the ideal
Linearization of Differential Equations for Approximation
On December 23, 2020 In Calculus, Mathematics for Machine Learning
In this post we learn how to build linear approximations to non-linear functions and how to measure the error between our approximation and the desired function. Given a well-behaved higher-order function, we can find an approximation using Taylor series. But how do we know when our approximation is good enough so that we can