Products, Quotients, and Chains: Simple Rules for Calculus

In this post, we are going to explain the product rule, the chain rule, and the quotient rule for calculating derivatives. We derive each rule and demonstrate it with an example.

The product rule allows us to differentiate a function that includes the multiplication of two or more variables. The quotient rule enables us to differentiate functions with divisions. With the chain rule, we can differentiate nested expressions.

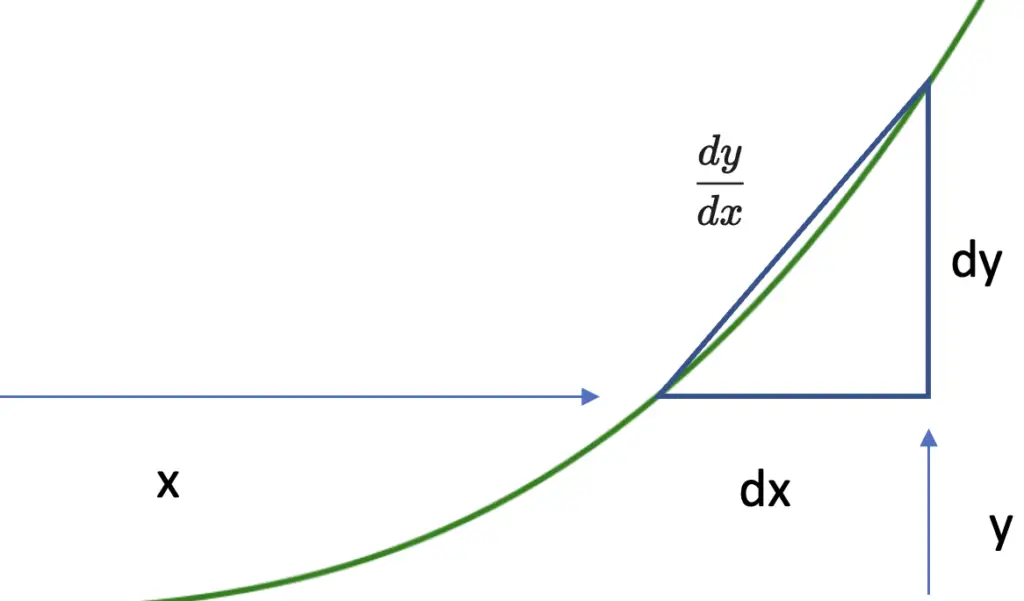
Before diving into the rules, let’s briefly recall what we are actually trying to calculate when applying these rules. As discussed in the post on rise over run, the derivative of some non-linear function is the slope of an infinitesimally small section at a particular point. For example, if we increase x by the small section dx, the slope tells us how much we can expect y to change (by dy).
That slope or derivative can be described as a ratio:

\frac{dy}{dx}

For the purpose of illustration, the triangle in the following illustration is drawn large, but it is actually infinitesimally small which means that for practical purposes it equals zero.

Chain Rule

The chain rule tells us how to obtain the derivative of a nested function y with respect to x like the following one.

y = y(u(x))

We can split the composite expression into two individual functions:

y = y(u)\\
u = u(x)

You obtain the derivative of the composite function by

• differentiating y with respect to u
• differentiating u with respect to x
• multiplying the two resulting expressions.

\color{red}\pmb{ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} }

If you want to see proof of why this works, I’d recommend checking out the following video by turksvids.

Example: Chain Rule

Let’s show how the chain rule works with an example. We start with the function y. To simplify, we substitute the inner term with a third variable u. This has the effect of breaking the composite function into two separate functions.

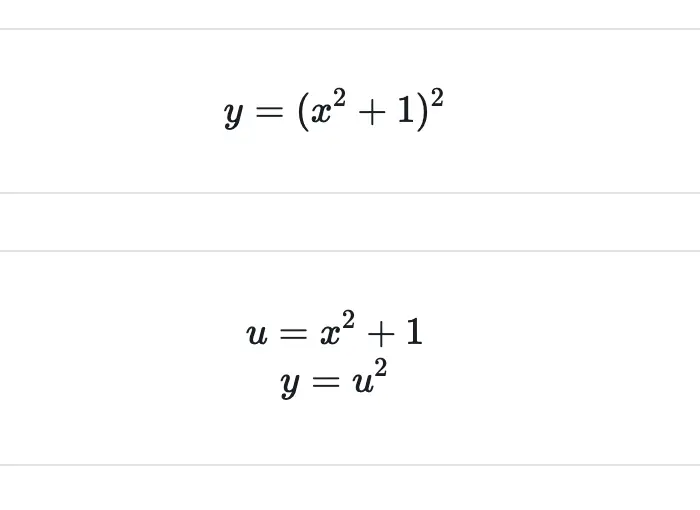
Let’s differentiate u and y individually and add them together.

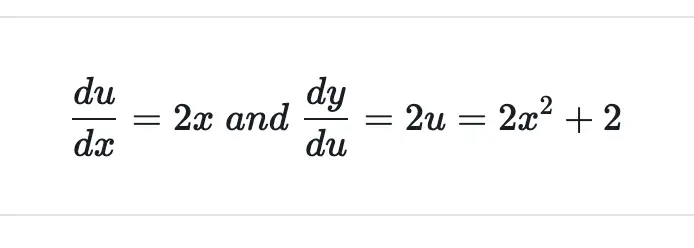
Substituting this into our formula, we get

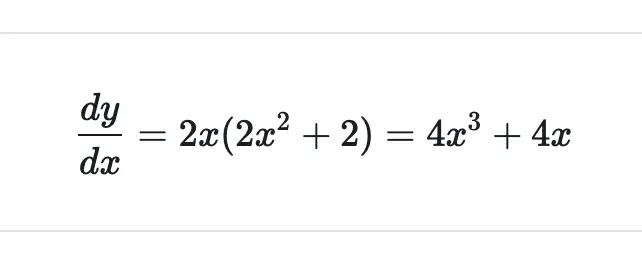
To check whether this is true, we can solve the same problem without the chain rule by multiplying it out before we differentiate. This isn’t equivalent to rigorous proof, but it is sufficient for most practical calculus applications.

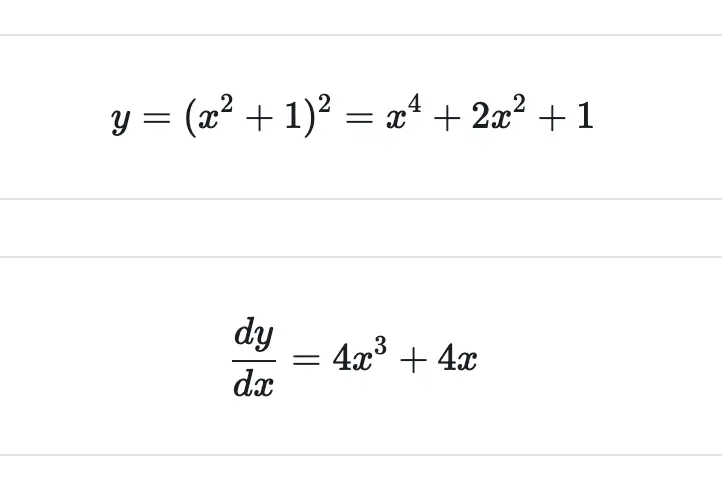
They give us the same answer.

Product Rule

Assume we have the following equation involving a simple multiplication.

y = u \times v

To obtain that section and the corresponding slope, we grow the components u and v by infinitesimally small amounts du and dv. This results in:

y + dy = (u + du) \times (v + dv)

To find the derivative, dy/dx, we need to find a way to relate this expression to dy/dx. Notice, that the term already has dy, so we still need dx.

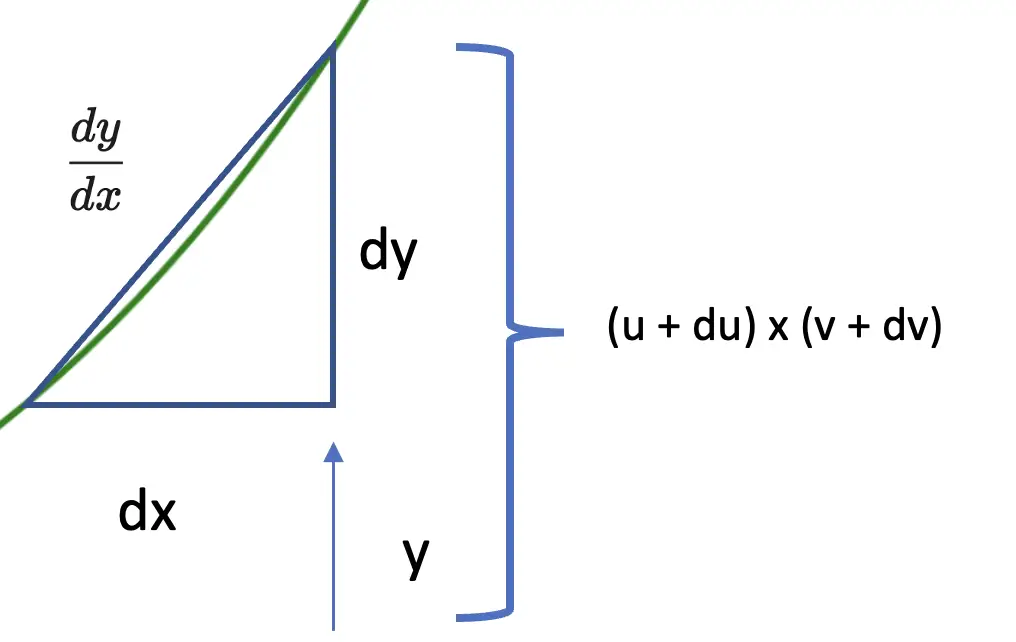
If we multiply this expression out, we arrive at the following.

y + dy = u \times v + u\times du + v\times dv + du\times dv

Remember that dx and dy were infinitesimally small so that they practically equal 0. The expressions du and dv were only fractions of the already small dy. If we multiply du and dv, the resulting term becomes even smaller. In fact, the term dudv is so small that we can safely ignore it and thus eliminate it from the equation.
The term u x v is equivalent to y, so we can subtract it from both sides of the equation. Now, we are left with this expression.

dy = u\times dv + v \times du

Remember when we said that we still need dx. We can bring it in now by simply dividing both sides of the expression by dx which won’t change the overall value.

 \color{red}\pmb{ \frac{dy}{dx} =u \frac{dv}{dx} + v\frac{ du}{dx} }

The result has our expression for the derivative on the left and relates it to the factors u and v on the right. In other words, it tells us how to differentiate a function that includes the multiplication of two variables.

Congratulations, we just derived the product rule. To obtain the derivative of a function that multiplies two factors, multiply the first factor by the derivative of the second factor and add the second factor multiplied by the derivative of the first factor.

The Triple Product Rule

Of course, the product rule can be applied to functions including more than two factors.

y = u \times v \times w

Growing y by the infinitesimally small section gives us the following expression:

y + dy = (u + du) \times (v + dv)  \times (w + dw)

Doing the arithmetic as in the previous section, we end up with the following expression for the triple product rule:

\frac{dy}{dx} = vw\frac{ du}{dx} + uw \frac{dv}{dx} + uv \frac{dw}{dx}

The product rule can similarly be expanded to cover four or even more factors.

Example: Product Rule

Let’s do some examples to see how it works in practice

Example: Product Rule with Two Factors

The rest is just simple arithmetic, that you can do for yourself if you want.

Example: Triple Product Rule and Chain Rule

y = x^2(1-x)^3e^{-x}

Here we have a term consisting of three factors. To take the derivative of it we need to apply the triple product rule.

\frac{dy}{dx} = (1-x)^3e^{-x}\frac{d(x^2)}{dx} + x^2e^{-x}\frac{d((1-x)^3)}{dx} 

+ x^2(1-x)^3\frac{d(e^{-x})}{dx}

First Chain Rule Application

So far so good. But to differentiate this expression, we need to take care of a nested term (1-x)^3. This requires an application of the chain rule. So let’s solve that term first by substituting u for the expression 1-x inside the brackets.

y = u^3 \;and\; u = 1-x 

  \frac{dy}{du} = 3u^2 \;and\; \frac{du}{dx} = -1

Now we can differentiate the inner term and multiply the two results together as stipulated by the chain rule.

\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}  = (3)(1-x)^2(-1)

Second Chain Rule Application

The derivative in the third term also requires the application of the chain rule.

\frac{d(e^{-x})}{dx}

We split the term.

y = e^u \;and\;u=-x

Now we can differentiate the terms separately. Note that the derivative of the exponential e^u is e^u.

\frac{dy}{du} = e^u \;and\; \frac{du}{dx} = -1

\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} = -e^u = -e^{-x}

Continuing the Full Example…

With that out of the way, we can come back to the full example and resolve the derivatives.

\frac{dy}{dx} = 2x(1-x)^3e^{-x}+ x^2e^{-x}(3)(1-x)^2(-1) 

+ x^2(1-x)^3e^{-x}(-1)

Each term contains

x, (1-x)^2\; and\; e^{-x}

so we can factor these out.

\frac{dy}{dx} = x(1-x)^2 e^{-x} [ 2(1-x) -3x - x(1-x)]

Again, we could simplify further but since it is just simple arithmetic, we leave it at that.

Quotient Rule

With the chain rule and the product rule under our belt, we are now well equipped to calculate a derivative with the quotient rule.

Let’s say we want to differentiate the following function.

y = \frac{u}{v}

This is equivalent to

y = (u)(v)^{-1}

From now on I will denote derivatives of a variable v as v‘.

The term v^{-1} is a nested term with v being the inner term and -1 the “shell”. To get its derivative, we have to apply the chain rule.

(v^{-1})' =  -1v^{-2}v'

Now we can apply the product rule to get the derivative of y denoted by y‘.

y' = u(v^{-1})' + u'v =-1v^{-2}v'u + u'v^{-1}

Let’s tidy up a bit and put the terms with negative powers back into the denominator.

y' = -\frac{v'u}{v^{2}} + \frac{u'}{v^{1}} 

Finally, we can multiply the right term by v to get the same denominator and simplify as follows.

\color{red}y' = -\frac{v'u}{v^{2}} + \frac{u'v}{v^{2}}  = \frac{u'v-v'u }{v^{2}}

Example: Quotient Rule

Now that we’ve derived the quotient rule for calculating derivatives successfully, we only need to take the terms of our function y and substitute them into the derived formula.

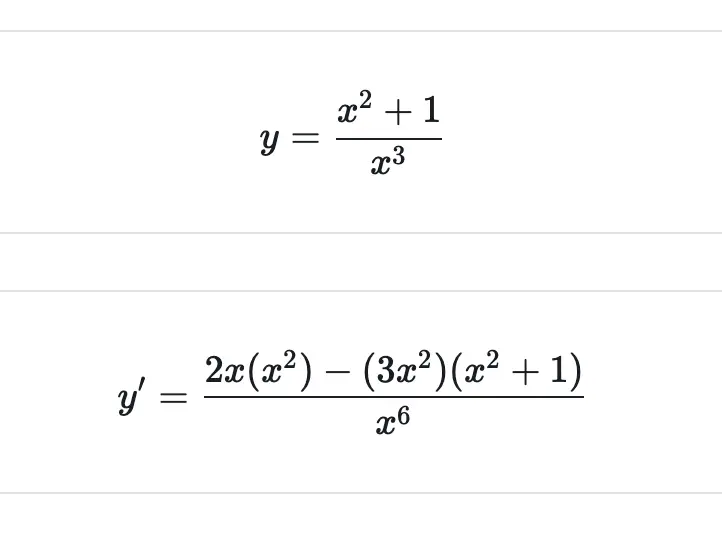
This post is part of a series on Calculus for Machine Learning. To read the other posts, go to the index.