Computer Vision Archive

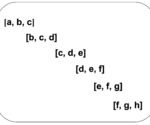
The sliding window algorithm is a method for performing operations on sequences such as arrays and strings. By using this method, time complexity can be reduced from O(n3) to O(n2) or from O(n2) to O(n). As the subarray moves from one end of the array to the other, it looks like a sliding window.

In this post, we will cover the foundations of how neural networks learn to localize and detect objects. Object Localization vs. Object Detection Object localization refers to the practice of detecting a single prominent object in an image or a scene, while object detection is about detecting several objects. A neural network can localize

In this post, we will develop a practical understanding of deep learning for image segmentation by building a UNet in TensorFlow and using it to segment images. What is Image Segmentation? Image Segmentation is a technique in digital image processing that describes the process of partitioning an image into sections. Often the goal is

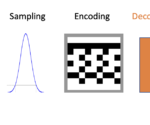
What is an Autoencoder? An autoencoder is a neural network trained to compress its input and recreate the original input from the compressed data. This procedure is useful in applications such as dimensionality reduction or file compression where we want to store a version of our data that is more memory efficient or reconstruct

In this post, we will develop a foundational understanding of deep learning for image classification. Then we will look at the classic neural network architectures that have been used for image processing. Deep Learning for Image Classification Image classification in deep learning refers to the process of getting a deep neural network to determine

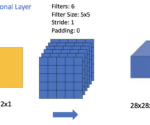
In this post, we understand the basic building blocks of convolutional neural networks and how they are combined to form powerful neural network architectures for computer vision. We start by looking at convolutional layers, pooling layers, and fully connected. Then, we take a step-by-step walkthrough through a simple CNN architecture. Understanding Layers in a

Pooling in convolutional neural networks is a technique for generalizing features extracted by convolutional filters and helping the network recognize features independent of their location in the image. Why Do We Need Pooling in a CNN? Convolutional layers are the basic building blocks of a convolutional neural network used for computer vision applications such

Padding describes the addition of empty pixels around the edges of an image. The purpose of padding is to preserve the original size of an image when applying a convolutional filter and enable the filter to perform full convolutions on the edge pixels. Stride in the context of convolutional neural networks describes the process

This post will introduce convolutional kernels and discuss how they are used to perform 2D and 3D convolution operations. We also look at the most common kernel operations, including edge detection, blurring, and sharpening. A convolutional filter is a filter that is applied to manipulate images or extract structures and features from an image.

In this post, we build an intuitive step-by-step understanding of the convolution operation and develop the mathematical definition as we go. A convolution describes a mathematical operation that blends one function with another function known as a kernel to produce an output that is often more interpretable. For example, the convolution operation in a