Understanding Padding and Stride in Convolutional Neural Networks
Padding describes the addition of empty pixels around the edges of an image. The purpose of padding is to preserve the original size of an image when applying a convolutional filter and enable the filter to perform full convolutions on the edge pixels.
Stride in the context of convolutional neural networks describes the process of increasing the step size by which you slide a filter over an input image. With a stride of 2, you advance the filter by two pixels at each step.
In this post we will learn how padding and stride work in practice and why we apply them in the first place.
Why Do We Need Padding?
When performing a standard convolution operation, the image shrinks by a factor equivalent to the filter size plus one. If we take an image of width and height 6, and a filter of width and height 3, the image shrinks by the following factor.
6 - 3 +1 =4
The reason for the shrinking image is that a 3×3 filter cannot slide all three of its columns over the first two horizontal pixels in the image. The same problem exists with regard to the rows and the vertical pixels.
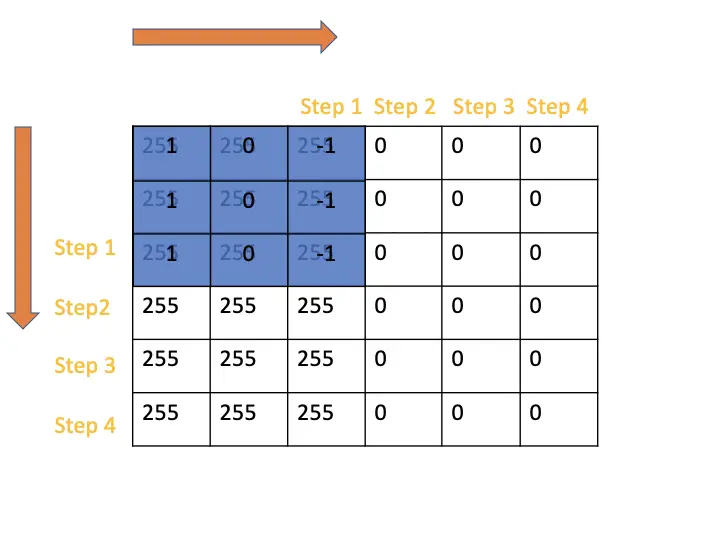
There are only 4 steps left for the filter until it reaches the end of the image, both vertically and horizontally. As a consequence, the resulting image will only have 4×4 dimensions instead of 6×6. The general formula for calculating the shrinkage of the image dimensions m x m based on the kernel size f x f, can be calculated as follows:
(m\times m) * (f\times f) = (m-f+1)*(m-f+1)
This immediately entails two problems:
- If you perform multiple convolution operations consecutively, the final image might become vanishingly small because the image will shrink with every operation.
- Because you cannot slide the full filter over the edge pixels, you cannot perform full convolutions. As a result you will lose some information at the edges.
The problem becomes more pronounced as the size of the filter increases. If we use a 5 x 5 filter on the 6 x 6 image, we only have space for 2 convolutions.
To address these problems, we can apply padding.
How Does Padding Work?
To mitigate the problems mentioned above, we can pad our images with additional empty pixels around the edges.
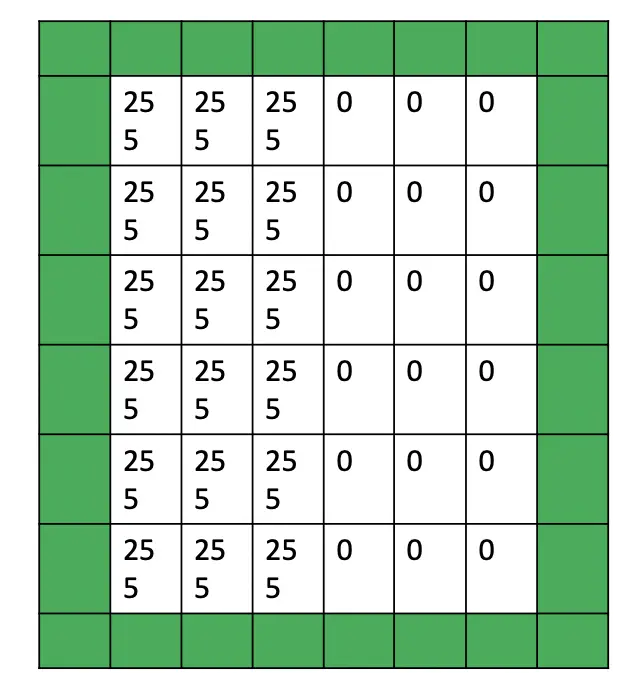
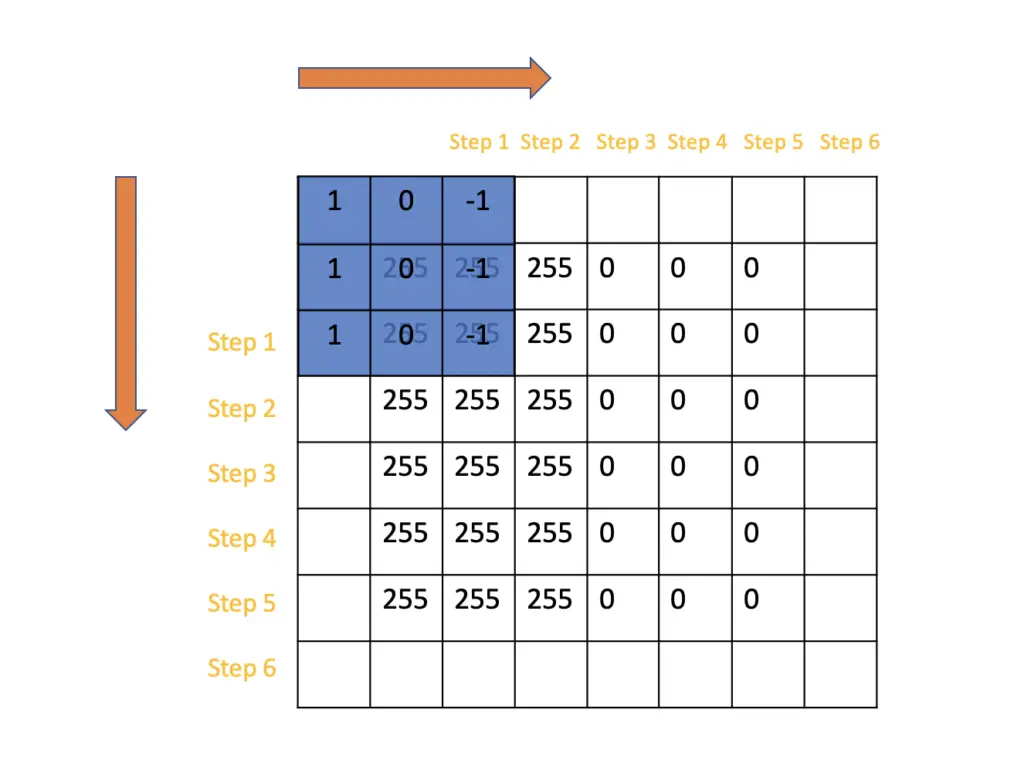
If we apply a 3×3 filter, we can slide it by 6 steps in every direction. The resulting feature map of the convolutional operation preserves the 6×6 dimensions of the original image.
Same Padding
Same padding is the procedure of adding enough pixels at the edges so that the resulting feature map has the same dimensions as the input image to the convolution operation.
In the case of a 3×3 filter, we pad each edge with one string of pixels. If we had a 5×5 filter, we would have to pad each edge with two rows/columns of pixels.
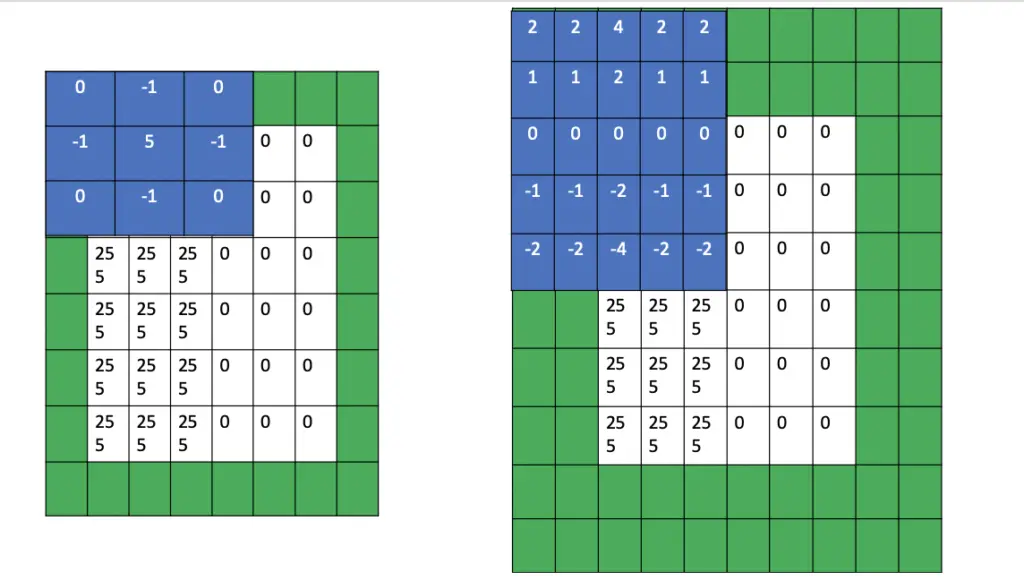
In summary, how many pixels you use for same padding depends entirely on the size of the filter. The most commonly used filter sizes are 3×3, 5×5, and 7×7. If your filter size is odd, you can calculate the pixels you need on each side by subtracting 1 from the filter size and dividing the result by 2. The division by 2 is necessary because you want to distribute the pixels evenly on both sides of the image.
padding = \frac{f-1}{2}Valid Padding
Valid padding means that we only apply a convolutional filter to valid pixels of the input. Since only the pixels of the original image are valid, valid padding is equivalent to no padding at all.
How Do Strided Convolutions Work?
The stride simply describes the step size when sliding the convolutional filter over the input image. In the previous examples, we’ve always slid the filter by one pixel rightwards or downwards. We’ve used a stride of 1.
With a stride of 2, we would slide the window by two pixels on each step.
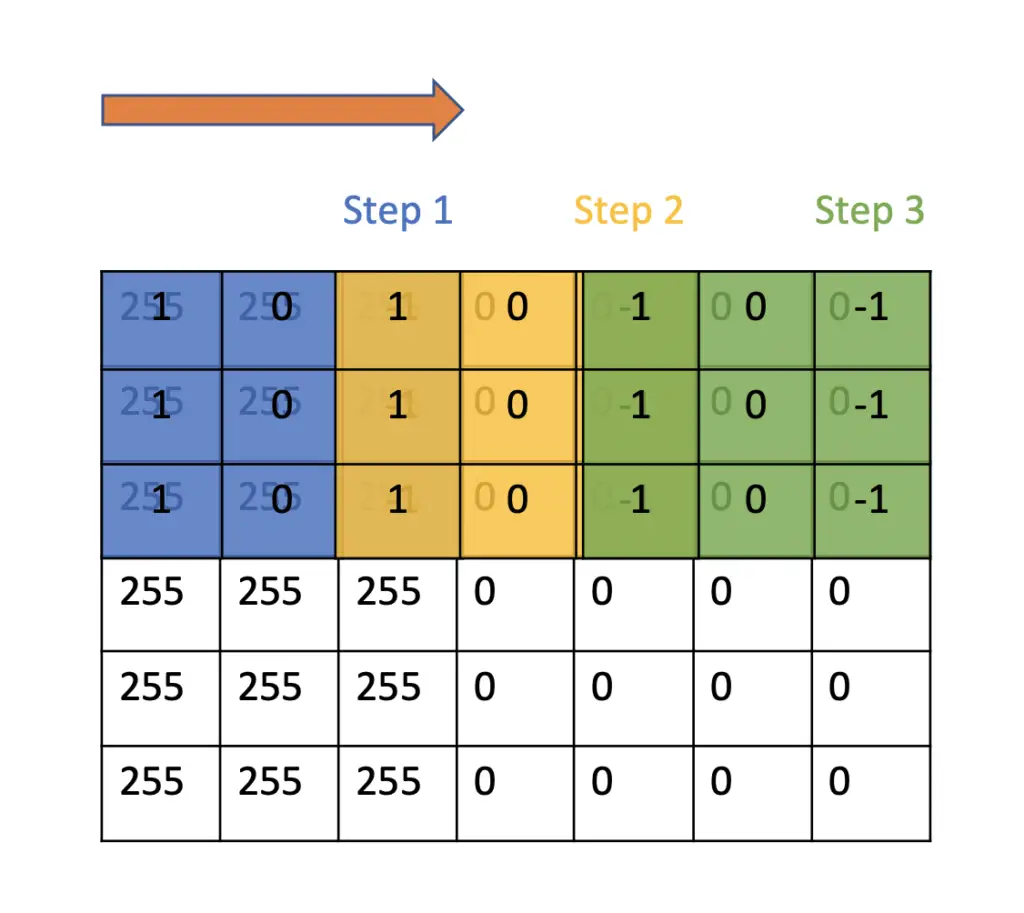
Since we are taking larger steps, we will reach the end of the image in fewer steps. As a consequence, the resulting feature map will be smaller since the feature map directly depends on the number of steps we take.
If we slide a few 3×3 filters over a 7×7 image, we can only take two steps until we reach the end of the image. Counting the initial position of the filter as another step, we can only take 3 steps resulting in a 3×3 output map. As demonstrated in the post on convolutional filters, we multiply each pixel value with its corresponding filter value and sum up the products. In the following image, we have a sharp transition from white to black pixels running vertically through the image, indicating that there must be an edge.
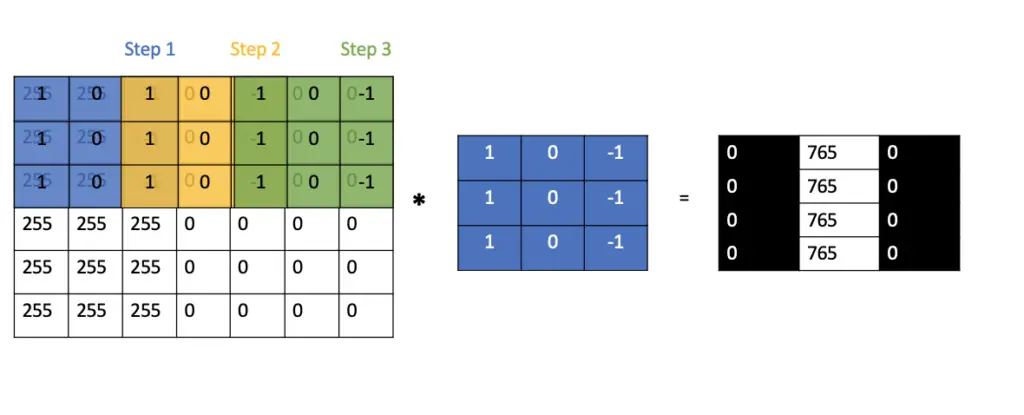
We can calculate the length of the output feature map o depending on the filter length size f, the length of the original image m and the stride s as follows.
o = \frac{n-f}{s} + 1Why Do We Need Strided Convolutions?
Generally speaking, the smaller the steps you take when sliding the filter over an image, the more details will be reflected in the resulting feature map. It also means that more features will be shared between the outputs since large portions of the filters will overlap.
For example, when applying a 3×3 filter that is always moved by 1 pixel, a filter will share 2/3 of the input pixels with each adjacent filter.
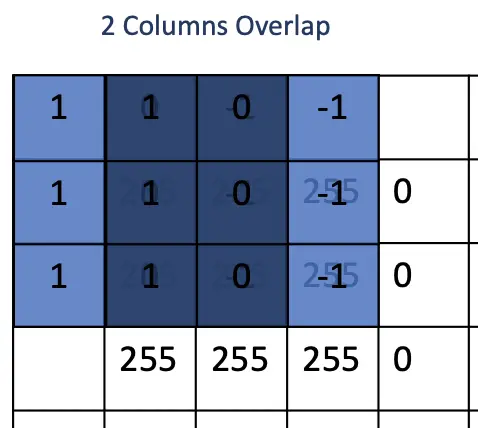
If we increase the step size, fewer parameters are shared between filters, and the feature map is smaller. Applying a larger stride basically has the effect of downsampling the image so that lower level details are obscured.
Furthermore, the more filter operations we want to calculate, the more computational power we need. If our neural network only requires an understanding of higher level features, we can make the learning process computationally more efficient by choosing a larger stride.
These considerations stem from the early days of deep learning when computational power was a major obstacle to efficient neural network training. With the ability to train neural networks on large and extremely potent GPU clusters in the cloud, increasing the stride to improve computational efficiency has become largely unnecessary. In practice, many modern deep learning practitioners use a stride of 1.
Summary
Padding and stride are two techniques used to improve convolutions operations and make the more efficient. Same padding is especially important in the training of very deep neural network. If you have a lot of layers, it becomes increasingly difficult to keep track of the dimensionality of the outputs if the dimensions change in every layer. Furthermore, the size of the feature maps will be reduced at every layer resulting in information loss at the borders. This is likely to depress the performance of your neural network.
Stride, on the other hand, has lost its importance in practical applications due to the increase in computational power available to deep learning practitioners.
This article is part of a blog post series on deep learning for computer vision. For the full series, go to the index.