What is the Sliding Window Algorithm?

The sliding window algorithm is a method for performing operations on sequences such as arrays and strings. By using this method, time complexity can be reduced from O(n3) to O(n2) or from O(n2) to O(n). As the subarray moves from one end of the array to the other, it looks like a sliding window.

First, we need to define a window that meets the requirements of the challenge. On an array or string, we can delimit a subsection called a window using two pointers – say, left and right.
Using the sliding window approach, we can perform actions on specific parts of linear sequences. An array’s “windows” consist of a series of continuous sequences. The window is slid over the array, as the name implies. The window gets slid further once some actions are taken on the elements within it.
You can enlarge the window by incrementing and decrementing the pointers that define the window.

Sliding Windows in Computer Vision

A sliding window in computer vision refers to a rectangular region with a defined width and height that moves over an image.

Sliding windows play a crucial role in object classification, as they allow us to localize exactly “where” in an image an object sits. Utilizing both a sliding window and an image pyramid, we can recognize objects in photographs at various scales and places.

Normally, we’d use an image classifier on the window region to see if it contains an object of interest. By combining sliding windows with object classification, we can build classification systems for images that can identify objects of various sizes and positions. Despite their simplicity, these techniques are the foundation of modern neural network architectures for identifying objects in images.

When to Use the Sliding Window Approach?

The following are some of the most important indications that a sliding window approach might be appropriate:

• Your problem involves data structures such as arrays, lists, and strings. An image is basically a multidimensional array
• You want to find a subrange involving the longest, shortest, or goal values in that array or string.
• Conceptually, it revolves around ideas like the longest or shortest sequence of something that meets a specific requirement.

How the Sliding Window Algorithm Works

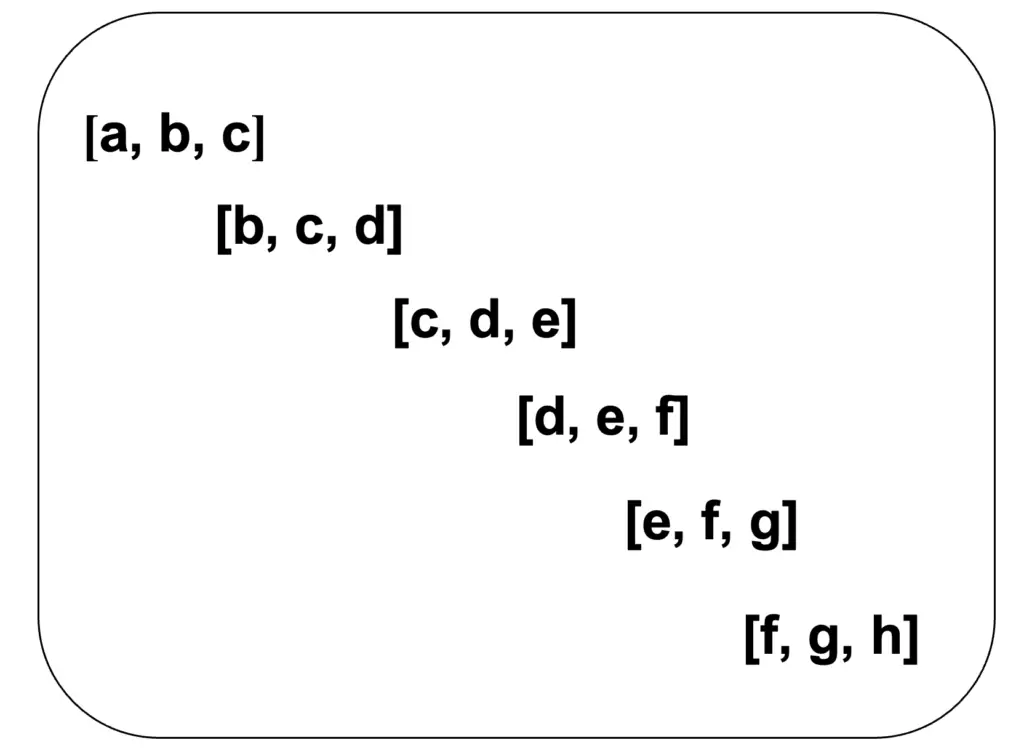
Consider the following array as an example:

[a, b, c, d, e, f, g, h]

A sliding window would pass over the array as follows.

The sliding window technique operates according to the following steps:

• Determine the required window size.
• Begin with the data structure’s first window.
• In a loop, slide the window by 1 and continue calculating the result window by window.

Here is an example of how the sliding window approach can be used to find the largest sum of all the successive integers in an n-item array of integers:

Naive Approach: Let’s look at an algorithmic implementation for solving this problem using the brute force approach. We begin at the first index and work our way up to the kth element. We do that for every single successive block of k elements. The outer for loop begins with the first element of the k-element block, and the inner or nested loop adds up to the k^th element of the block. 

# O(n * k) solution for finding
# maximum sum of a subarray of size k
INT_MIN = -sys.maxsize - 1

# Returns maximum sum in a
# subarray of size k.
def maxSum(arr, n, k):

	# Initialize result
	max_sum = INT_MIN

	# Consider all blocks
	# starting with i.
	for i in range(n - k + 1):
		current_sum = 0
		for j in range(k):
			current_sum = current_sum + arr[i + j]

		# Update result if required.
		max_sum = max(current_sum, max_sum)

	return max_sum


# Driver code
arr = [1, 4, 2, 10, 2,
	3, 1, 0, 20]
k = 4
n = len(arr)
print(maxSum(arr, n, k))
# Output = 24

The time complexity of the preceding code is O(k*n) because it has two nested loops.

Using a sliding window of length n, we can solve the same problem in a linear time frame. If we start from scratch, the pane will be located at the very left, 0 units from the left. Slide the window over the array arr[] of size n and calculate the current sum of size k elements. Now, we push the window forward by a unit of distance, as shown. After each step, the next k items will be covered by the pane.

Applying sliding window technique:

• We use a simple loop to compute the sum of the k components under the window and store it in the variable window_sum.
• While moving through the array, we keep tabs on the maximum total found inside a window.
• To calculate the current sum of a block of k items, either sum up all the items under the window or subtract the first element from the previous block and add the last element of the current block.

Let’s look at a step-by-step example of how the window slides over the data set.
Consider an array arr[] = {5, 2, -1, 0, 3} and value of k = 3 and n = 5

Here we have calculated the initial window total from index 0 onwards. The window sum is six at this point. Using the current window as the maximum sum, we may set the maximum sum to 6.

After that, we move our window by one unit. As a consequence, it now removes 5 from the window and adds 0 at the end. We deduct 5 from our new window sum before adding 0. Now, the new value of our window sum is 1. This window sum will be compared to the current maximum sum. We won’t adjust the maximum sum because it’s smaller than the current maximum.

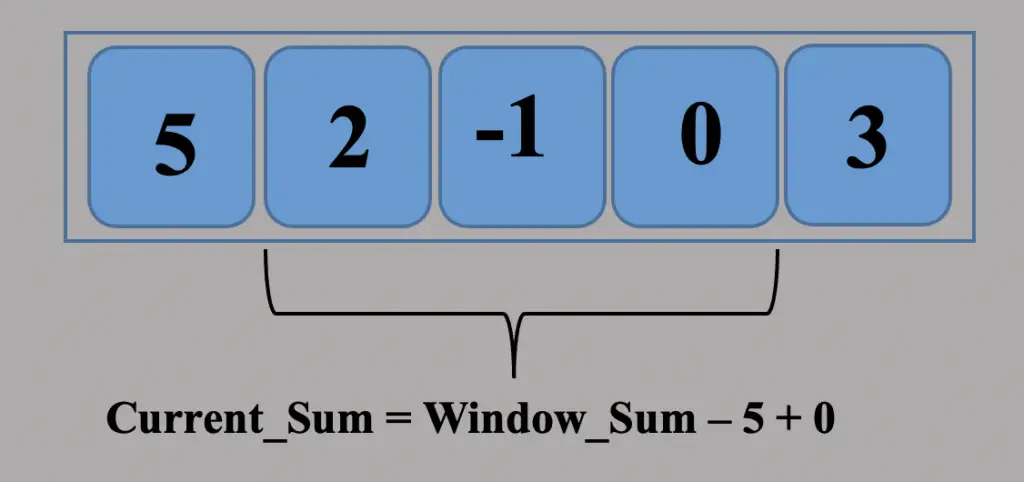
This time we move our window by a unit index to get the new window sum of 2. Once more, we check if the current window sum exceeds the maximum sum reached thus far. The maximum sum is not changed because the current sum is smaller than the maximum.

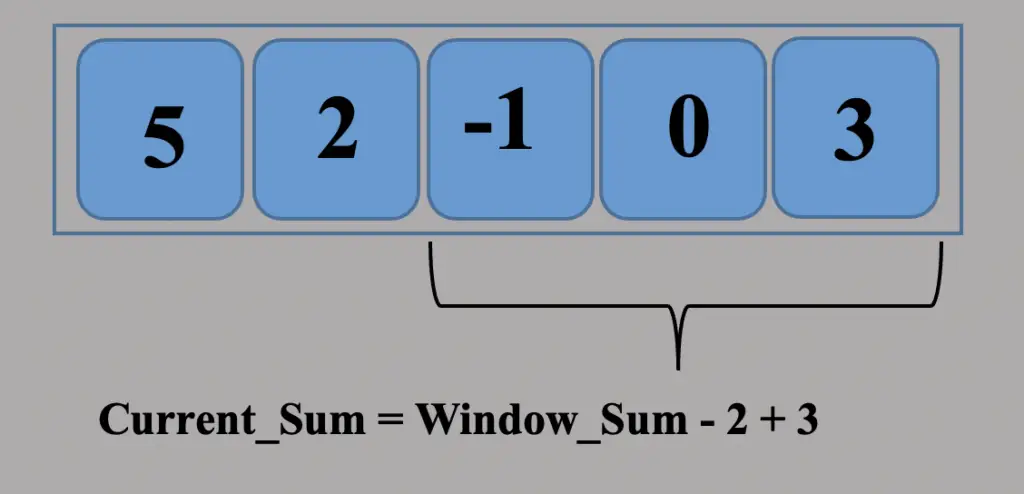
This array’s maximum sum, thus, is 6.

A code implementation of this approach would look like this:

# O(n) solution for finding
# maximum sum of a subarray of size k


def maxSum(arr, k):
	# length of the array
	n = len(arr)

	# n must be greater than k
	if n < k:
		print("Invalid")
		return -1

	# Compute sum of first window of size k
	window_sum = sum(arr[:k])

	# first sum available
	max_sum = window_sum

	# Compute the sums of remaining windows by
	# removing first element of previous
	# window and adding last element of
	# the current window.
	for i in range(n - k):
		window_sum = window_sum - arr[i] + arr[i + k]
		max_sum = max(window_sum, max_sum)

	return max_sum


# Driver code
arr = [1, 4, 2, 10, 2, 3, 1, 0, 20]
k = 4
print(maxSum(arr, k))

# Output = 24

As you may have recognized, there is just one loop in our code. Our Time Complexity is linear O(n).

Conclusion

The sliding window is more of a method than a formula. Algorithms of all kinds can be enhanced using sliding windows. The sliding window method is useful for reducing the time complexity of certain problems. The method can be used to solve almost any problem that fits the requirement of being able to add items sequentially or in parallel into one variable. For example, it allows us to tackle problems like calculating the maximum sum of n numbers. Compared to the brute-force approach, the sliding window algorithm computes the current sum in fewer steps. We can use this pattern for other problems as well.