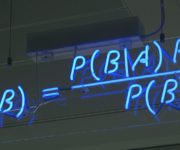Probability and Statistics Archive
Maximum Likelihood Estimation for Gaussian Distributions
On February 1, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we learn how to derive the maximum likelihood estimates for Gaussian random variables. We’ve discussed Maximum Likelihood Estimation as a method for finding the parameters of a distribution in the context of a Bernoulli trial, Most commonly, data follows a Gaussian distribution, which is why I’m dedicating a post to likelihood
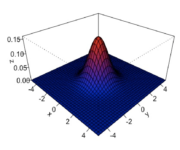
Multivariate Gaussian Distribution
On January 30, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we discuss the normal distribution in a multivariate context. The multivariate Gaussian distribution generalizes the one-dimensional Gaussian distribution to higher-dimensional data. In the absence of information about the real distribution of a dataset, it is usually a sensible choice to assume that data is normally distributed. Since data science practitioners deal
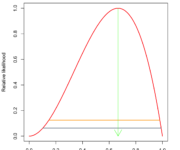
Maximum Likelihood Estimation Explained by Example
On January 23, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we learn how to calculate the likelihood and discuss how it differs from probability. We then introduce maximum likelihood estimation and explore why the log-likelihood is often the more sensible choice in practical applications. Maximum likelihood estimation is an important concept in statistics and machine learning. Before diving into the specifics,
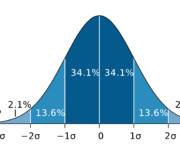
Normal Distribution and Gaussian Random Variables
On January 21, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we introduce the normal distribution and its properties. We also learn how to calculate Z scores and standard deviations from the mean. The normal distribution also known as the Gaussian distribution is the most commonly used probability distribution. The normal distribution curve has the famous bell shape. Many real-world random variables
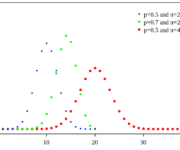
Bernoulli Random Variables and the Binomial Distribution in Probability
On January 18, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we develop an understanding of Bernoulli random variables and the binomial distribution. We introduce scenarios that follow the binomial distribution and learn how it relates to the normal distribution. The Bernoulli Distribution A Bernoulli random variable can be used to model the probability of a system whose outcome can only result
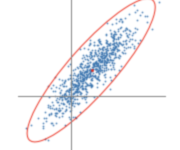
Covariance and Correlation
On January 15, 2021 In Mathematics for Machine Learning, Probability and Statistics
Int this post, we introduce covariance and correlation, discuss how they can be used to measure the relationship between random variables, and learn how to calculate them. Covariance and Correlation are both measures that describe the relationship between two or more random variables. What is Covariance The formal definition of covariance describes it as
Introducing Variance and the Expected Value
On January 13, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we are going to look at how to calculate expected values and variances for both discrete and continuous random variables. We will introduce the theory and illustrate every concept with an example. Expected Value of a Discrete Random Variable The expected value of a random variable X is usually its mean.
The Law of Total Probability and Bayesian Inference
On January 9, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we introduce the law of total probability and learn how to use Bayes’ rule to incorporate prior probabilities into our calculation for the probability of an event. Events don’t happen in a vacuum. They are related to and dependent on circumstances in their environment. Bayes rule allows us to relate the
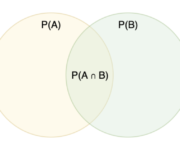
Conditional Probability and the Independent Variable
On January 8, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post we learn how to calculate conditional probabilities for both discrete and continuous random variables. Furthermore, we discuss independent events. Conditional Probability is the probability that one event occurs given that another event has occurred. Closely related to conditional probability is the notion of independence. Events are independent if the probability of
Probability Mass Function and Probability Density Function
On January 6, 2021 In Mathematics for Machine Learning, Probability and Statistics
In this post, we learn how to use the probability mass function to model discrete random variables and the probability density function to model continuous random variables. Probability Mass Function: Example of a Discrete Random Variable A probability mass function (PMF) is a function that models the potential outcomes of a discrete random variable.