What is Batch Normalization And How Does it Work?

Batch normalization is a technique for standardizing the inputs to layers in a neural network. Batch normalization was designed to address the problem of internal covariate shift, which arises as a consequence of updating multiple-layer inputs simultaneously in deep neural networks.

What is Internal Covariate Shift?

When training a neural network, it will speed up learning if you standardize your data to a similar scale and normalize its mean and variance. Otherwise, gradient descent might take much more time to move along one dimension where data is on a larger scale as compared to another dimension with a smaller scale. For more information, check out my post on feature scaling and data normalization.

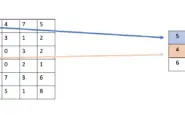
But even with standardized/normalized datasets, your distribution will shift as you propagate the data through the layers in a neural network. The reason is that in each iteration, we update the weights for multiple connected functions computed by the layers simultaneously. But updates to the weights for a particular function happen under the assumption that all other functions are held constant. Over many layers and iterations, this gradually leads to an accumulation of unexpected changes resulting in shifts in the data.

For example, if you have normalized your data to mean 0 and variance 1, the shape of the distribution may change as you propagate through the layers of your neural network.

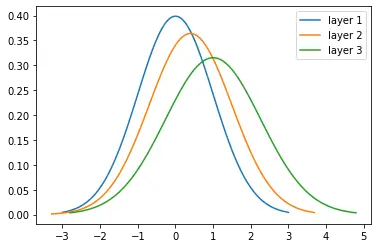
Mathematically, Goodfellow et al. illustrate this phenomenon with a simple example in their book “Deep Learning”. Ignoring the non-linear activation functions and the bias term, every layer multiplies the input by a weight w. Moving through 3 layers, you get the following output.

\hat y = xw_1w_2w_3

During backpropagation, we subtract the gradient times a learning rate from every weight.

\hat y = x(w_1-\alpha g_1)(w_2 - \alpha g_2)(w_3 - \alpha g_3)

If the weights are larger than 1, the computed term will grow exponentially. Even the subtraction of a small term in earlier layers has the potential to significantly affect updates to the later layers. This makes it uniquely hard to choose an appropriate learning rate.

How Batch Normalization Works

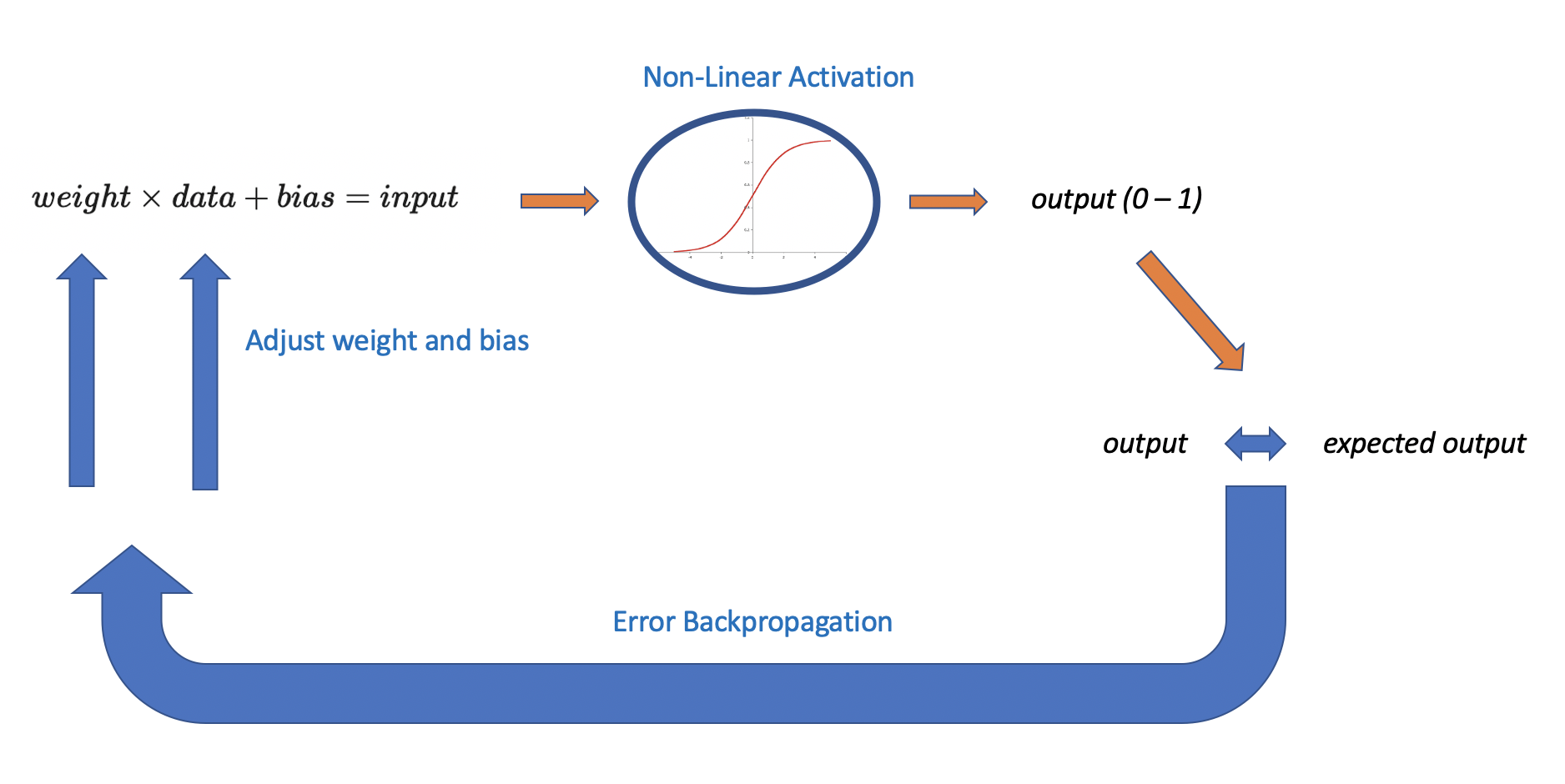
Batch norm addresses the problem of internal covariate shift by correcting the shift in parameters through data normalization. The procedure works as follows.

You take the output a^[i-1] from the preceding layer, and multiply by the weights W and add the bias b of the current layer. The variable I denotes the current layer.

z^{[i]} = W^{[i]} a^{[i-1]} + b^{[i]}  

Next, you would usually apply the non-linear activation function that results in the output a^[i] of the current layer. When applying batch norm, you correct your data before feeding it to the activation function.

Note that some researchers apply batch normalization after the non-linear activation function, but the convention is to do it before. We stick with the conventional use.

To apply batch norm, you calculate the mean as well as the variance of your current z.

\mu = \frac{1}{m} \sum_{j=1}^m z_j

When calculating the variance, we add a small constant to the variance to prevent potential divisions by zero.

\sigma^2 = \frac{1}{m} \sum_{j=1}^m (z_j-\mu)^2  + \epsilon

To normalize the data, we subtract the mean and divide the expression by the standard deviation (the square root of the variance).

z^{[i]} = \frac{z^{[i]}-\mu}{\sqrt{\sigma^2}}

This operation scales the inputs to have a mean of 0 and a standard deviation of 1.

An important consequence of the batch normalization operation is that it neutralizes the bias term b. Since you are setting the mean equal to 0, the effect of any constant that has been added to the input prior to batch normalization will essentially be eliminated.

Changing Mean and Standard Deviation

If we want to change the mean of the input, we can add a constant term β to all observations after batch normalization.

z^{[i]} = z^{[i]} + \beta

To change the standard deviation, we similarly multiply each observation with another constant γ.

z^{[i]} = \gamma z^{[i]}

In programming frameworks like Tensorflow, γ and β are tunable hyperparameters that you can set on the BatchNormalization layer.

Adjusting Batch Normalization at Test and Inference Time

In practice, we commonly use mini-batches for training neural networks. This implies that we are calculating the mean and variance for each mini-batch when applying batch normalization. Depending on the size of your mini-batch, your mean and variance for single mini-batches may differ significantly from the global mean and variance. For example, if you are using a mini-batch size of 8 observations, it is possible that you randomly pick 8 observations that are far apart and thus give you a higher variance.
This doesn’t matter so much at training time since you are using many mini-batches whose statistical deviations from the global mean and variance average each other out.

At test and inference time, you are typically feeding single observations to the model to make predictions. It doesn’t make sense to calculate the mean and variance for single observations. Due to the problems described in the previous paragraph, you also cannot simply take a mini-batch from the test set and calculate it’s mean and variance. Furthermore, you have to assume that you only get single examples at inference time. So calculating the mean and variance of the entire test dataset is also not an option.

Instead, people commonly either calculate the mean and variance on the entire training set or a weighted average across the mini-batches and use that at test time. If the training set is large enough, the statistics should be representative of the data the model will encounter at test and inference time (otherwise, the whole training process wouldn’t make much sense).

Why Batch Norm Works

As stated previously, deep neural networks suffer from internal covariate shifts where the distribution of data changes. By normalizing the data after each layer, we effectively rescale the data back to a standard normal distribution (or a distribution with the mean and variance set in the hyperparameters).

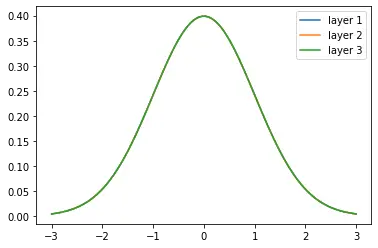
In practice, adding batch normalization has been demonstrated to speed up learning by requiring fewer training steps and a larger learning rate. It also has a regularizing effect that, in some cases, makes dropout redundant.

Bringing the shift in the data distribution under control is believed to be the main factor behind batch normalization’s success. However, some researchers argue that this is a misunderstanding, as the authors of the following paper.

This article is part of a blog post series on the foundations of deep learning. For the full series, go to the index.