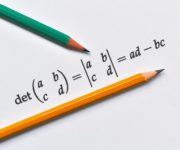None Archive

In this post we build an intuitive understanding of the Gamma distribution by going through some practical examples. Then we dive into the mathematical background and introduce the formulas. The gamma distribution models the wait time until a certain number of continuously occurring, independent events have happened. If you are familiar with the Poisson

This series of blog posts introduces probability and mathematical statistics. While I wrote these posts with a focus on machine learning and data science applications, they are kept sufficiently general for other readers. Some familiarity with vectors and matrices, as well as differential and integral calculus, is necessary to fully understand all concepts. If

We introduce and discuss the applications and properties of the diagonal matrix, the upper triangular matrix, and the lower triangular matrix. A diagonal matrix is a square matrix in which all entries are zero, except for those on the leading diagonal. It is also called the scaling matrix because multiplication with the diagonal matrix

We introduce Gaussian elimination and Gauss Jordan Elimination, more commonly known as the elimination method, and learn to use these methods to solve linear equations with several unknown variables. We also introduce the row echelon form of a matrix and discuss the difference between Gaussian elimination and Gauss Jordan elimination. Gaussian Elimination Method Gaussian

We introduce the matrix determinant and its uses. Furthermore, we learn how the determinant provides us with a shortcut to finding the inverse matrix. What is the matrix determinant? The determinant is a scalar value that can be obtained from a square matrix and which can be used to find the inverse of a

We learn how to construct transformation matrices and how to use them to rotate, stretch or otherwise transform vectors. A transformation matrix scales, shears, rotates, moves, or otherwise transforms the default coordinate system. In the process it maps coordinates from the current coordinate system to the one that resulted out of the transformation. A