Matrix and Array in Python NumPy

In this post, we discuss single- and multidimensional arrays and matrices in Python. Since Python does not offer in-built support for arrays, we use NumPy, Python’s library for matrix and array computations. The NumPy array is one of the most versatile data structures in Python and it is the foundation of most Python-based data science and machine learning applications.

What is an Array in Python?

A Python array is a collection of elements of the same data type. Each element in the array has a unique index and is stored at a contiguous location in memory.

How to Create a NumPy Array?

To create an array, you first have to install and import the NumPy module. If you haven’t installed it yet, check out the official installation guide.
Next, we import NumPy and create our first array containing the numbers 1-3. When we check the data type, Python tells us that this is a NumPy array.

import numpy as np

a = np.array([1, 2, 3])
type(a) # numpy.ndarray

Python Array vs List

Contrary to an array, a list does not constrain you to one data type. For example, you can store a string, an integer, and a boolean in a list like this:

l = ["string", 1, True]
print(l) # ['string', 1, True]

If you try to to the same with NumPy array, Python will attempt to represent all elements in the same data type. If we create an array with a string, an integer, and a boolean, all elements will be printed as strings and the data type is displayed as Unicode:

a = np.array(["string", 1, True])
print(a) # array(['string', '1', 'True'], dtype='<U6')

You can easily convert a NumPy array to a list using the list constructor.

a = np.array([1, 2, 3])
l = list(a)
print(l) #[1, 2, 3]

Conversely, you can also convert a list to a NumPy array using the array constructor.

l = ["string", 1, True]
a = np.array(l)
print(a) #['string' '1' 'True']

NumPy 2D Array and Matrix

Matrices and vectors with more than one dimensions are usually represented as multidimensional arrays in Python.

A NumPy 2D array in Python looks like a list nested within a list.

a_2d = np.array([[1,2,3], [4,5,6]])
type(a_2d)

How to Find the Array Length in Python

For a one-dimensional array, obtaining the array length or the size of the array in Python is fairly straightforward. You can just use the “len” function just as with a list.

a = np.array([1, 2, 3])
len(a) #3

If your array has more than one dimension, you can still use the “len” function but it will only return the length across the first dimension.

a_2d = np.array([[1,2,3], [4,5,6]])
len(a_2d) #2

To obtain the length of the array or matrix across all dimensions, we use what is known as the array shape in NumPy. The shape returns the array size regardless of the number of dimensions.

a_2d = np.array([[1,2,3], [4,5,6]])
print(a_2d.shape) #(2, 3)

How to Sort An Array in Python NumPy

NumPy has a sort function that operates like the inbuilt sort function which we used to sort lists. It can sort array elements either numerically, or alphabetically. By default, it sorts in ascending order.

a = np.array([3, 7, 4, 1])
print(np.sort(a)) #[1 3 4 7]

a = np.array(["c", "a", "b", "d"])
print(np.sort(a)) #['a' 'b' 'c' 'd']

If you try to sort a multidimensional array, it will sort the elements in the innermost array.

a_2d = np.array([
  [3,2,5], 
  [4,1,6]
])
print(np.sort(a_2d))

#[[2 3 5]
# [1 4 6]]

How to Concatenate Numpy Arrays

Concatenation in NumPy is done using the concatenate function. If you are dealing with two one-dimensional NumPy arrays, you can concatenate them by simply passing two arrays to the concatenate function. If you are dealing with multidimensional arrays, you have to specify the axis along which to concatenate.

You can concatenate a one-dimensional array as follows.

a1 = np.array([1, 2, 3])
a2 = np.array([4, 5, 6])
a_joined = np.concatenate((a1, a2))
print(a_joined)

Once you have higher-dimensional arrays, simply concatenating them is no longer enough. If you have experience with matrix addition in mathematics, you know that you can add matrices vertically or horizontally. With multidimensional arrays, you have the same problem. You need to decide along which axis to add the arrays.

But both matrices need to have the same size along the dimension that you add. You can only add a 2×3 matrix to a 2×2 matrix along the first dimension, because along the second dimension the first matrix has a size of 3, while the second has a size of 2.
In the NumPy concatenate function you can pass an axis argument. An axis argument of 0 tells Python to concatenate the matrices vertically.

a1 = np.array([[1, 2, 3], [4, 5, 6]])
a2 = np.array([[7, 8 ], [9, 10]])

a = np.concatenate((a1, a2), axis=0)
print(a)

This returns an error because the dimensions do not match vertically. If we instead concatenate horizontally, it works, because the dimensions match.

a1 = np.array([[1, 2, 3], [4, 5, 6]])
a2 = np.array([[7, 8 ], [9, 10]])

a = np.concatenate((a1, a2), axis=1)
print(a)

When Concatenating multidimensional arrays, you always have to be aware of how your dimensions fit together.

How does NumPy Delete Work?

The NumPy delete function takes the array and the index for the element you want to delete as arguments. For a multidimensional array you also need to specify the axis along which you want to delete elements. It returns a new array without the deleted elements.

For a one-dimensional array, deletion is fairly straightforward. We delete the second entry which has the index “1”:

a = np.array([1, 2, 3])
np.delete(a, 1) #array([1, 3])

For a multidimensional array, you have to add a third entry specifying the axis along which to delete. We delete the first entry with index 0. and we specify 0 for the axis, which corresponds to the horizontal axis.

a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]
             ]
            )
new_a = np.delete(a, 0, 0)
print(new_a)

Changing the axis to 1, we delete along the vertical axis which removes the first entry of each of the subarrays.

a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]
             ]
            )
new_a = np.delete(a, 0, 1)
print(new_a)

Matrix Operations in Python NumPy

Since NumPy arrays are the Pythonic way of representing matrices, you can perform mathematical matrix operations such as calculating transposes, inverses, and dot products.

How Do You Transpose a Matrix in Python NumPy?

You can transpose a matrix in NumPy using either the transpose function or using the dot T notation. Here is an example of how to perform transposes using both methods.

Using dot T notation:

a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]
             ]
            )

print(a.T)

Using the NumPy transpose function:

a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]
             ]
            )
print(np.transpose(a))

How Do You Find the Inverse of a Matrix in Python NumPy?

To find the inverse of a matrix, you can use NumPy’s module for linear algebra. You need to import the modules and then you can just pass the matrix to the inverse function as follows.

a = np.array([[1, 2, 3],
             [4, 5, 6],
             [7, 8, 9]
             ]
            )
la.inv(a)

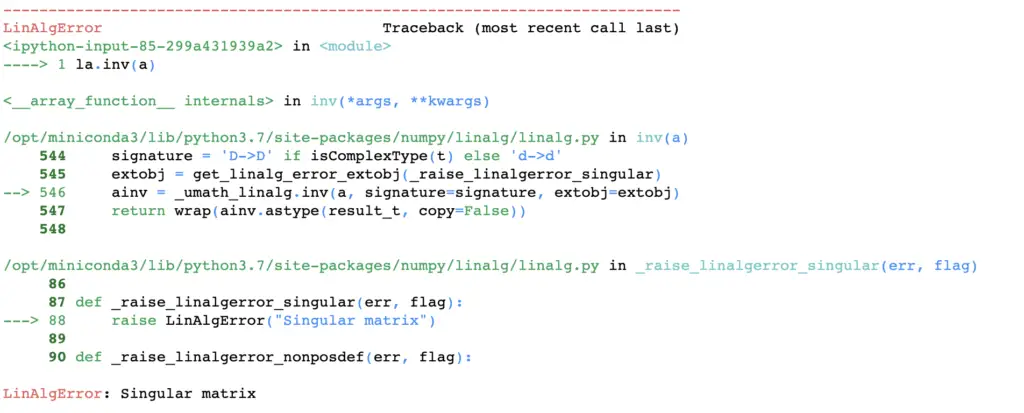
This will throw an error because the matrix is not invertible. Remember, that a matrix multiplied by its inverse needs to result in the identity matrix. Such an inverse may not exist depending on the original matrix. Let’s use another matrix that does have an inverse:

a = np.array([[4, 7],
              [2, 8],
             ]
            )
la.inv(a)

Now, the matrix is invertible and we get a result. If we calculate the dot product between the two matrices, we get the identity matrix.

Note that the upper-right value is not exactly zero due to Python’s floating point approximation.

How Do You Create an Identity Matrix in Python NumPy?

An identity matrix can be constructed with NumPy’s identity function. Since an identity matrix is a symmetric matrix with ones on the leading diagonal, and zeros everywhere else, NumPy only needs to know the number of dimensions to construct the matrix.

np.identity(3)

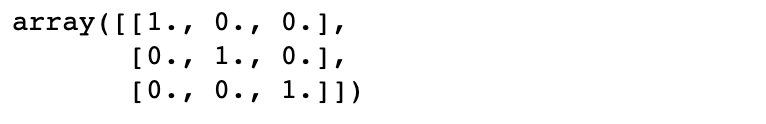
How Do You Calculate a Dot Product in NumPy

To calculate the dot product, you can use the np.dot function in NumPy. The function takes the two matrices or vectors as arguments that you want to dot.

a1 = np.array([[2, 2],
             [2, 2],
             [2, 2]
             ])

a2 = np.array([[3, 3],
             [3, 3],
            ])

np.dot(a1, a2)

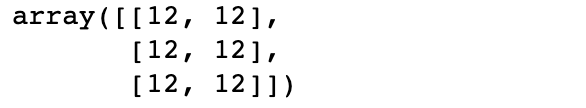
When you calculate dot products in linear algebra, you need to ensure that the horizontal axis of the first matrix has the same size as the vertical axis of the second matrix. If we try to change the order of the matrices in the previous calculation, we will get an error because the dimensions do not match.

a1 = np.array([[2, 2],
             [2, 2],
             [2, 2]
             ])

a2 = np.array([[3, 3],
             [3, 3],
            ])

np.dot(a2, a1)